Spirolaèdres

Cet article est la suite de cet article mathémaTICE sur les spirolatères.
On va se consacrer ici aux généralisations 3D des spirolatères.

                                                              modèle 1 pour N=11 et 1 itération

I) Présentation du problème

En 2D, pour construire un spirolatère "de base" on répète la même série d'étapes sur le modèle suivant (illustration tirée de l'article d'Yves Martin) :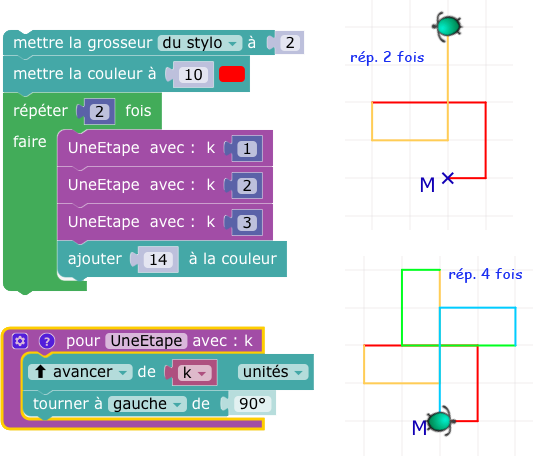

La question est de savoir comment on va adapter ce schéma en 3D.
Yves Martin propose alors l'adaptation suivante, qui consiste à superposer deux étapes élémentaires pour constituer une nouvelle étape élémentaire en 3D.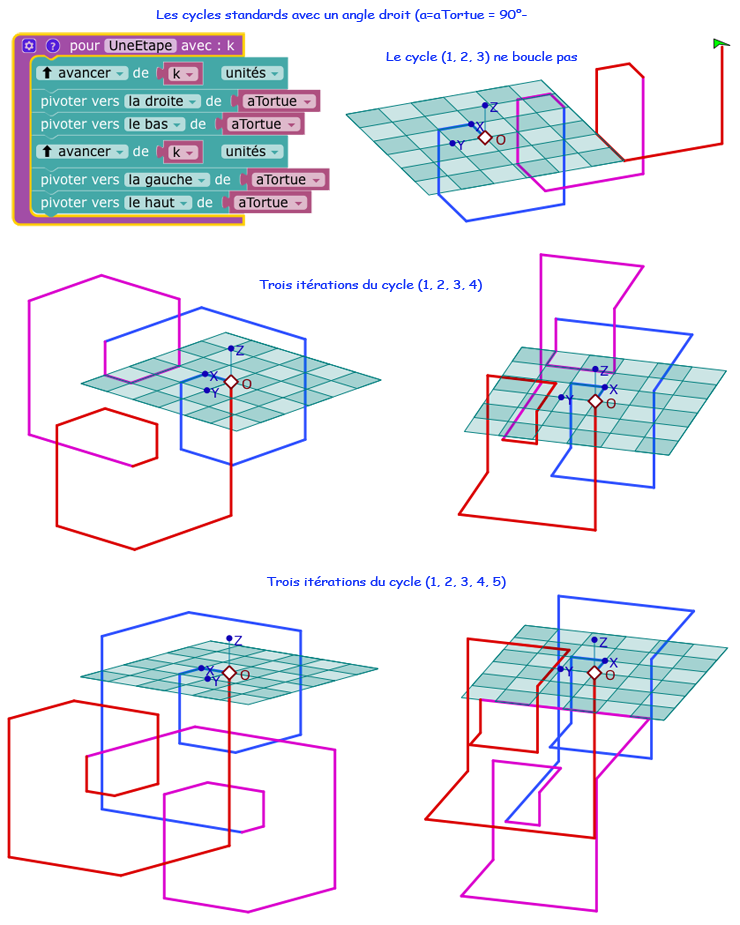

Une question posée est alors de savoir ce que va devenir le polygone des extrémités lors du passage en 3D, et en particulier si (jamais) le modèle va permettre aux extrémités de parcourir les sommets d'un polyèdre régulier.

Pour ce premier modèle proposé, les extrémités sont toujours soit coplanaires soit non périodiques et positionnées sur une hélice circulaire.
En effet, si on répète un bloc identique d'étapes de ce type, alors il existe une application qui permet de passer d'une extrémité à une autre (cette application traduit le sous programme répété), et cette application est :

• en 2D une rotation ou une translation
• en 3D un vissage (= ou une rotation ou une translation qui sont des cas particuliers)

Autrement dit, il existe une isométrie directe qui fait passer d'une extrémité à l'autre.

• En 2D, on passe d'un sommet d'un polygone régulier à un autre quand le spirolatère se referme.
• En 3D, on passe d'un point à un autre "régulièrement espacé" sur une hélice circulaire.

Et dans ce cas on a très peu de marge de liberté en ce qui concerne le parcours des extrémités (en particulier, il est exclu qu'elles puissent parcourir les sommets d'un polyèdre régulier).

On va donc procéder autrement en faisant en sorte, dans un premier temps, de garder un angle constant de 90° entre les segments, mais sans répéter une étape identique.

II) Nouveau modèle

Pour obtenir cet angle 3D constant (en mesure), on va enchaîner :

• PivoterHaut
• TounerGauche
• PivoterBas

avec des paramètres bien choisis.

On commence par une étude théorique de l'enchaînement de ces trois rotations :

• PivoterHaut(p1)
• TounerGauche(t)
• PivoterBas(p2)

Si (u,v,w) est le repère mobile initial, on obtient après application de PivoterHaut(p1) :

u'=u.cos(p1) + w.sin(p1)
v'=v
w'=-u.sin(p1)+w.cos(p1)

Après les trois rotations (et un peu de patience...), on obtient alors :

u''' = u.(cos(p1)cos(p2)cos(t)+sin(p1)sin(p2))+ v.sin(t)cos(p2) + w.(sin(p1)cos(t)cos(p2)-cos(p1)sin(p2))
v'''=-u.cos(p1)sin(t)+v.cos(t)-w.sin(p1)sin(t)
w'''=u.(cos(p1)sin(t)cos(p2)-sin(t)cos(p2)) + v.sin(t)sin(p2) + w.(sin(p1)sin(p2)cos(t)+cos(p1)cos(p2))

Si on veut que u et u''' fassent un angle de a° il faut alors que cos(p1)cos(p2)cos(t)+sin(p1)sin(p2) = cos(a).

C'est cette égalité que l'on va s'attacher à préserver.

II) A) Cas particulier : angle de 90°

On commence par le cas d'un angle de 90° entre les segments.

Si on veut que u et u''' fassent un angle de 90° il faut que cos(p1)cos(p2)cos(t)+sin(p1)sin(p2) = 0

soit cos(t) = -tan(p1)tan(p2)

On prend p1=90° et t=360°/N x nombre d'étapes écoulées.
Normalement, il faudrait donc prendre p2 = - Arctan(cos(t)/tan(p1)).
mais attention: p1=90° donc tan(p2) = -cos(t).cotan(p1)=0, autrement dit p2=0.

Voici le script CaRMetal (pour deux itérations).
(On renonce volontairement à introduire du magnétisme dans CaRMetal pour avoir des figures plus fluides.
On donnera des versions dynamiques DGPad un peu plus loin.)

fichier spirou-01.zirs en p-j

Et on peut ajouter quelques instructions pour construire le parcours des extrémités :

fichier spirou-02.zirs en p-j

Qu'est-ce que l'on obtient avec ce modèle ?

Pour N = 3 et une itération, on obtient cet abat-jour :

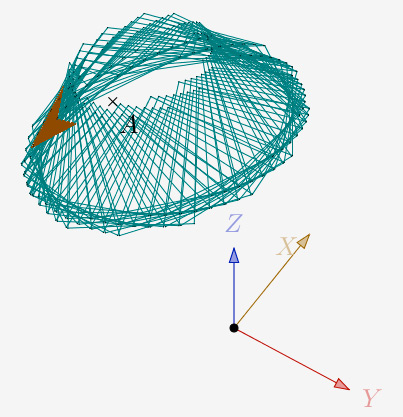
N = 3 et une itération

Pour N = 3 et deux itérations on obtient ce chapeau :

N = 3 et deux itérations

Si on ajoute le parcours des extrémités, on obtient :

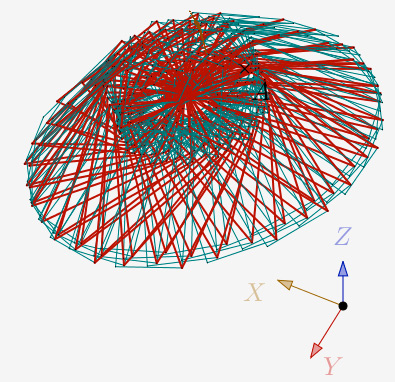
Pour N=3 et trois itérations, on obtient une figure qui ne boucle pas.

N = 3 et trois itérations

Pour quatre itérations:

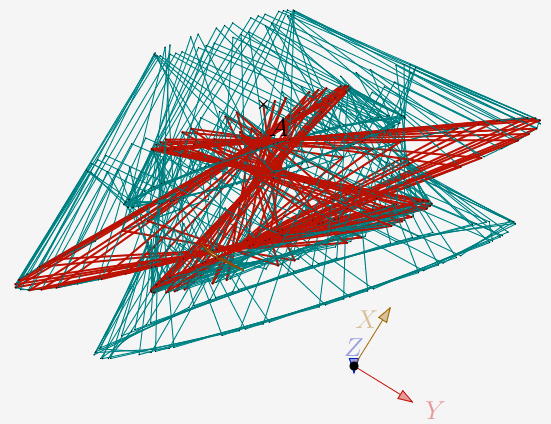
N = 3 et 4 itérations

Pour N=2,5 et une itération, on obtient un emporte-pièces en étoile.

N=2,5 et une itération

Ou plus exactement, on s'en approche comme on le voit sur la figure, et on peut alors chercher à affiner.
Mais c'est extrêmement instable! On a un effet papillon assez saississant.

Pour N=3,5 et une itération on obtient un vase:

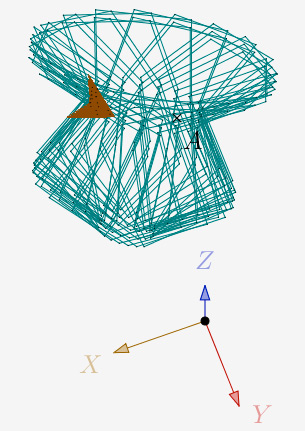
N=3,5 et une itération

Pour N=4,5 et deux itérations on obtient une roue de tracteur :

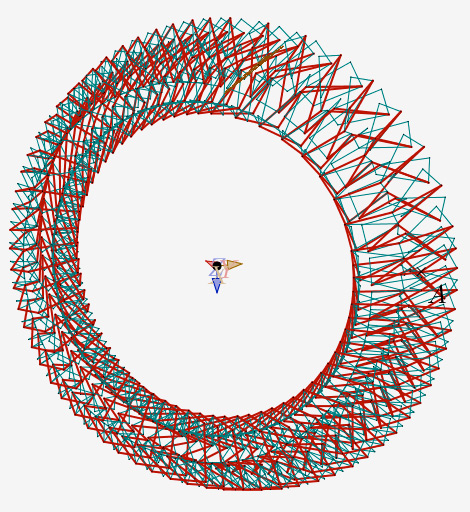
N=4,5 et deux itérations

Voici d'autres exemples en vrac :

N=4,5 et trois itérations

----------------------------------------------------------------------------------------

N=4,5 et quatre itérations

----------------------------------------------------------------------------------------

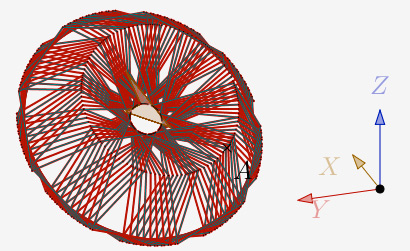
N=5 et une itération

----------------------------------------------------------------------------------------

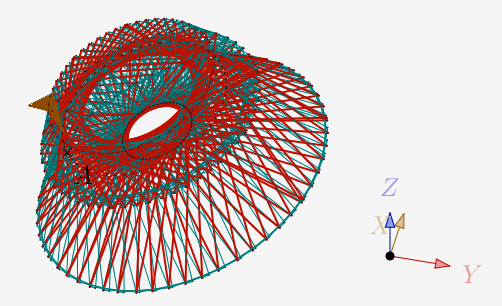
N=5 et deux itérations

----------------------------------------------------------------------------------------

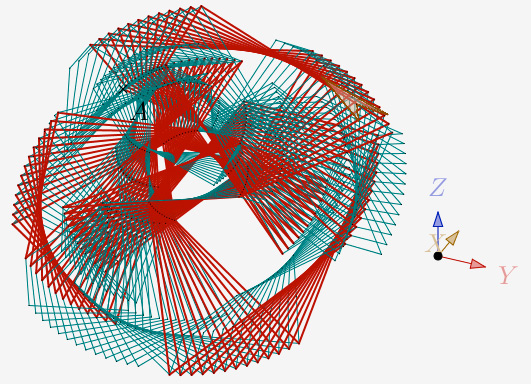
N=5 et 3 itérations

----------------------------------------------------------------------------------------

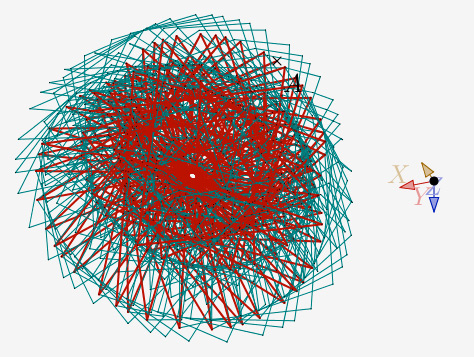
N=5 et 4 itérations

----------------------------------------------------------------------------------------

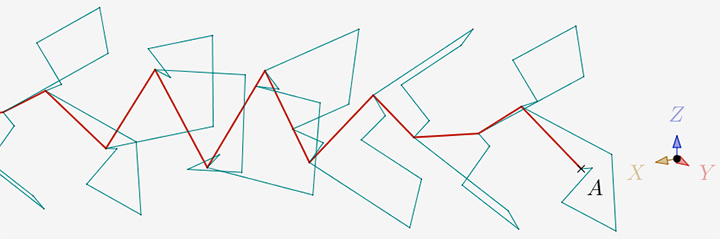
N=5 et 5 itérations

----------------------------------------------------------------------------------------

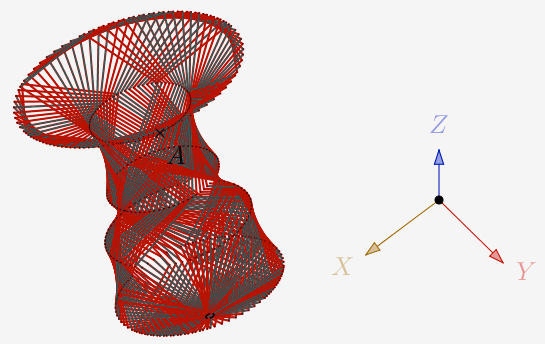
N=5,5 et 1 itération

----------------------------------------------------------------------------------------

Version dynamique avec DGPad

On a juste traduit le script CaRMetal en script DGPad.
Et on obtient le dynamisme "naturellement" car dans DGPad les scripts sont dynamiques par essence.
Par ailleurs, on a plus de puissance avec DGPad (on peut tracer plus d'étapes).

devient...

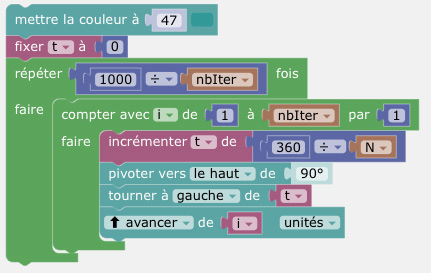
Traduire ce script CaRMetal en script DGPad se fait sans aucune difficulté (ce ne sera pas le cas pour le script avec le tracé supplémentaire du polygone des extrémités, qui est plus simple avec CaRMetal).
La difficulté principale consiste à mettre en place les différents éléments (3D, curseurs,...) selon la syntaxe de DGPad avant d'accéder à l'écriture du script. Pour présenter cette étape, on va le faire page suivante dans une petite vidéo (pour CaRMetal puis DGPad).

II) A) Cas particulier : angle de 90° / à propos de DGPad

Pour la version avec le polygone des extrémités, la version CaRMetal est comme on l'a vu :

Mais la tortue de DGPad n'étant pas complètement mutante, on ne peut pas procéder de cette façon.
On va donc reprendre la méthode d'Yves Martin présentée dans ce paragraphe de son article sur les spirolatères (onglet curseur et algèbre).

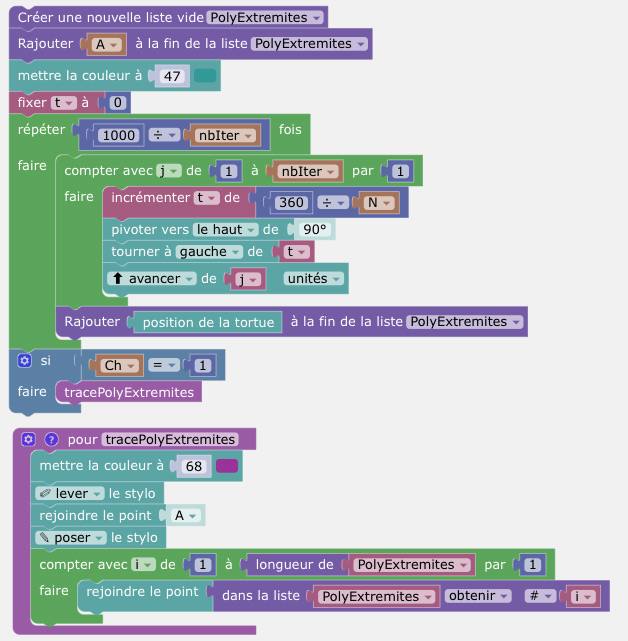
pour obtenir cette figure dynamique :

II) B) 1) Généralisation : angle constant entre les segments

Dans cette première généralisation, on veut  que u et u''' fassent un angle constant de de a°
Comme on l'a vu plus haut, il faut alors que cos(piv1)cos(piv2)cos(t)+sin(piv1)sin(piv2) = cos(a).

Si on veut généraliser le cas précédent, on pourrait prendre piv1=a et garder t comme précédemment.
Une autre généralisation consiste à prendre piv1 = 180 - a . Et c'est ce choix que l'on va faire. Ce qui donne ce script :

fichier spirou-03.zirs en p-j

fichier spirou-04.zirs en p-j (version avec parcours des extrémités)

On obtient alors certaines courbes fermées :

a = 120° et N=1,7 et 1 itération

---------------------------------------------------------------------------------

a = 120° et N=1,9 et 1 itération

---------------------------------------------------------------------------------

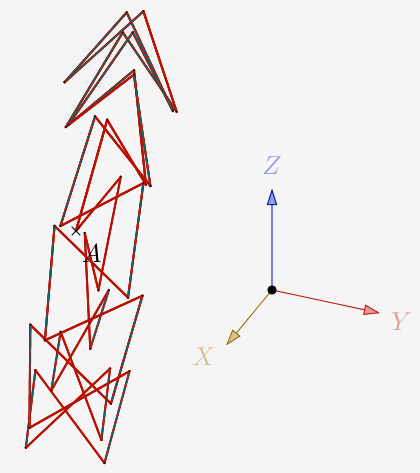
a = 120° et N=2,1 et 1 itération

---------------------------------------------------------------------------------

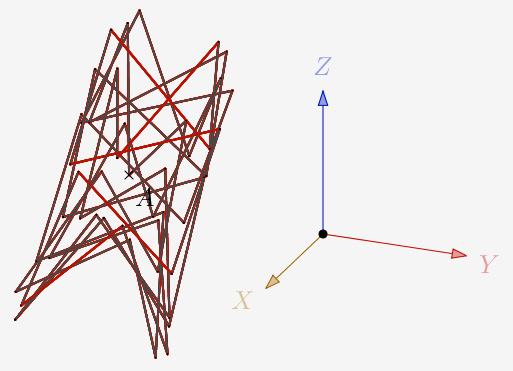
a = 120° et N=2,3 et 1 itération

---------------------------------------------------------------------------------

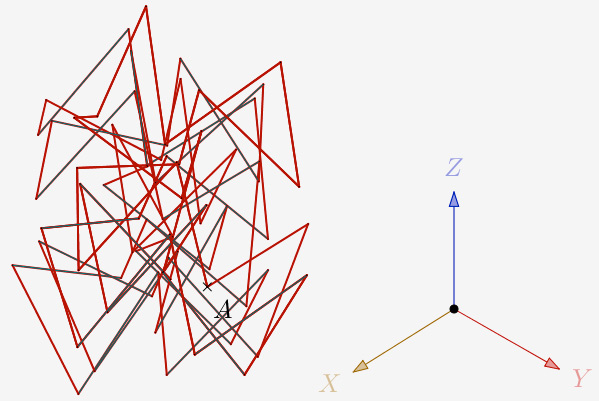
a = 120° et N=3,7 et 1 itération

---------------------------------------------------------------------------------

a = 120° et N=3,9 et 1 itération

---------------------------------------------------------------------------------

a = 120° et N=4,1 et 1 itération

---------------------------------------------------------------------------------

a = 120° et N=4,2 et 1 itération

---------------------------------------------------------------------------------

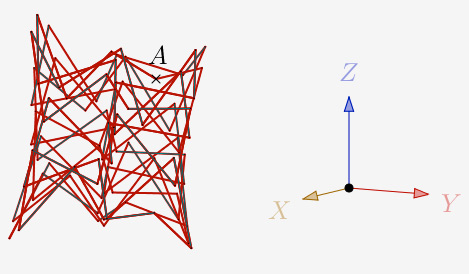
a = 120° et N=4,3 et 1 itération

---------------------------------------------------------------------------------

Certaines (beaucoup de) courbes ne sont pas fermées.

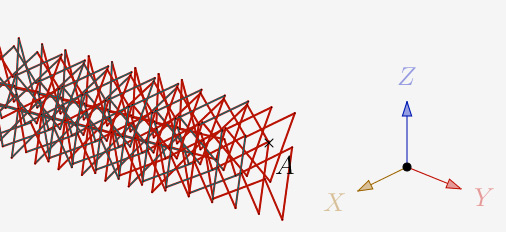
a = 120° et N=4,5 et 1 itération

---------------------------------------------------------------------------------

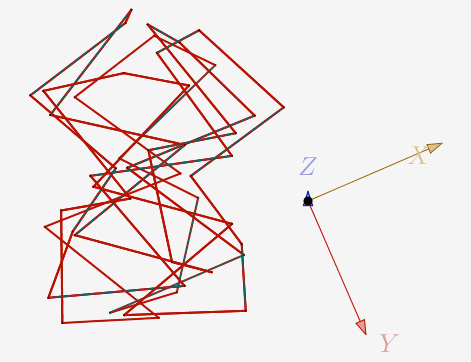
a = 120° et N=4,6 et 1 itération

--------------------------------------------------------------------------------

a = 120° et N=4,7 et 1 itération

--------------------------------------------------------------------------------

a = 120° et N=4,9 et 1 itération

--------------------------------------------------------------------------------

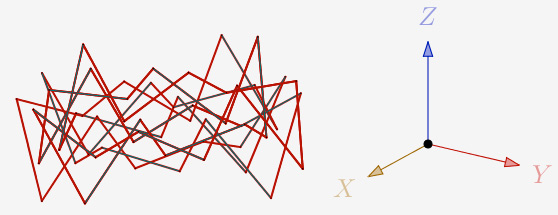
a = 120° et N=5,4 et 1 itération

--------------------------------------------------------------------------------

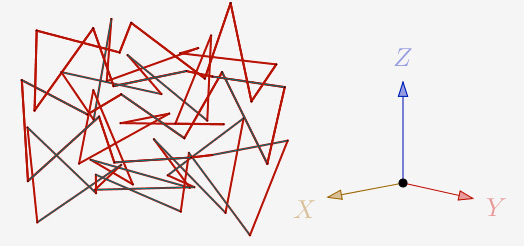
a = 120° et N=5,8 et 1 itération

--------------------------------------------------------------------------------

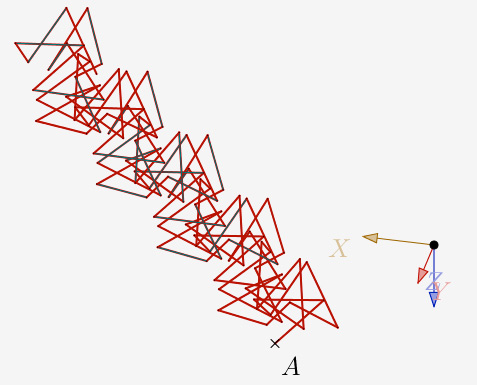
a = 120° et N=6 et 1 itération

--------------------------------------------------------------------------------

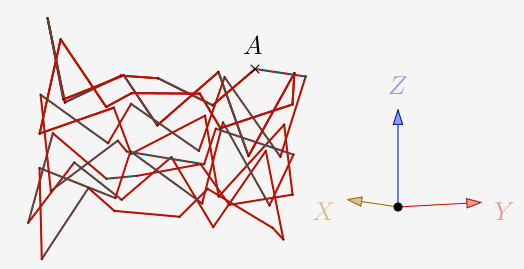
a = 120° et N=6,2 et 1 itération

-------------------------------------------------------------------------------

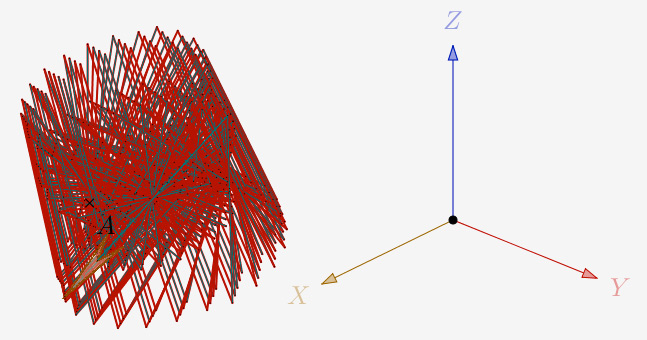
a = 135° et N=0,8 et 1 itération

--------------------------------------------------------------------------------

On est confronté à un problème : dans certain cas (= pour certaines valeurs de a et de N), il n'y a pas de solution pour conserver un angle de a° avec PivoterHaut(a) et TournerGauche(t). "Aïe!"...
En pratique, le procédé ne fonctionne que pour un angle a entre 41 et 139° (ou entre 221 et 319°).
La version dynamique DGPad n'a pas la même fluidité que précédemment.

II) B) 2) Généralisation : angle pas constant entre les segments / modèle 1

Une généralisation moins évidente consiste à calculer une fois pour toute l'angle piv2 tel que PivoterHaut(a), TournerGauche(a) et PivoterBas(piv2) fasse tourner en faisant un angle a (dans le cas de a=90° cet angle est 0°) puis à appliquer PivoterHaut(a), TournerGauche(t) et PivoterBas(piv2). Voici le script :

fichier spirou-05.zirs en p-j

fichier spirou-06.zirs en p-j (version avec parcours des extrémités)

L'angle entre les segments n'est pas constant, mais on a une bonne généralisation du cas a=90°.

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Variante

Comme piv2 ne dépend pas de t, on peut aussi penser à inverser les instructions Avancer et PivoterBas comme ceci :

fichier spirou-07.zirs en p-j

fichier spirou-08.zirs en p-j (version avec parcours des extrémités)

Le script peut alors être simplifié/compressé de la façon suivante :

fichier spirou-07b.zirs en p-j

fichier spirou-08b.zirs en p-j (version avec parcours des extrémités)

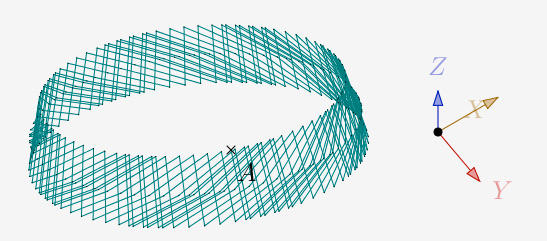
a = 45° et N=3 et 1 itération

---------------------------------------------------------------------------------

a = 60° et N=3 et 1 itération

---------------------------------------------------------------------------------

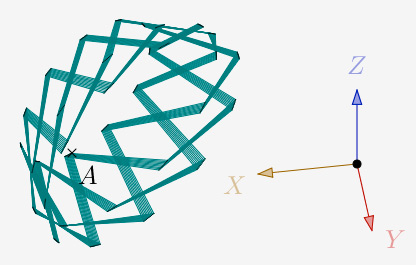
a = 72° et N=3 et 1 itération

---------------------------------------------------------------------------------

a=120° et N=3 et 1 itération

---------------------------------------------------------------------------------

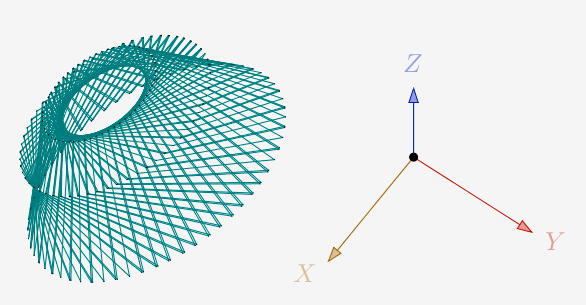
a=225° et N=3 et 1 itération

---------------------------------------------------------------------------------

a=240° et N=3 et 1 itération

---------------------------------------------------------------------------------

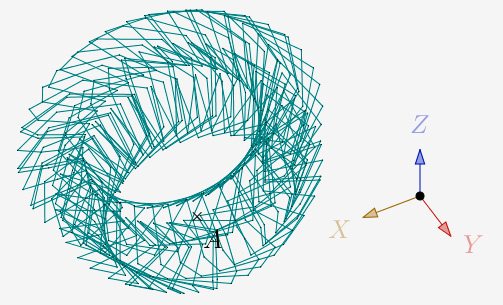
a=60° et N=5,5 et 1 itération

---------------------------------------------------------------------------------

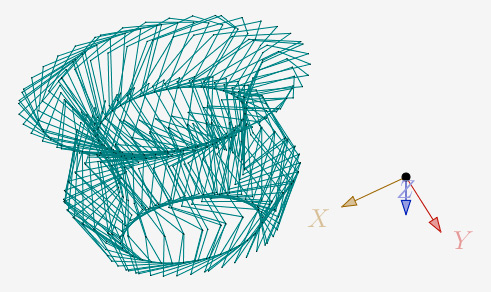
a=72° et N=5,5 et 1 itération

---------------------------------------------------------------------------------

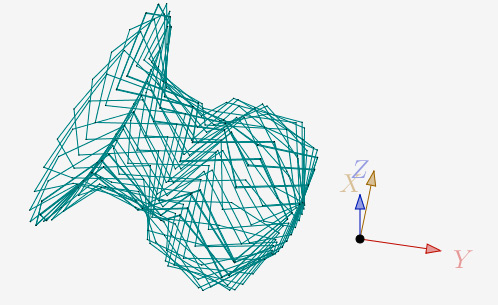
a=120° et N=5,5 et 1 itération

---------------------------------------------------------------------------------

a=135° et N=5,5 et 1 itération

---------------------------------------------------------------------------------

a=210° et N=5,5 et 1 itération

---------------------------------------------------------------------------------

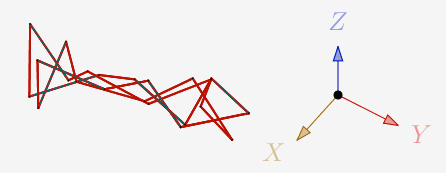
a=225° et N=5,5 et 1 itération

---------------------------------------------------------------------------------

II) B) 2) Généralisation : angle pas constant entre les segments / modèle 2

Une autre généralisation consiste simplement à prendre comme précédemment

• PivoterHaut(piv1)
• TounerGauche(t)
• PivoterBas(piv2)

mais à supprimmer simplement PivoterBas(piv2)

Ce qui donne ce script CaRMetal :

fichier spirou-09.zirs en p-j

fichier spirou-10.zirs en p-j (version avec parcours des extrémités)

Pièces jointes :

spirolaedres.zip [zip avec 12 figures CaRMetal]

spiro_DGPad.zip [zip avec 4 figures DGPad]

Présentation rapide de DGPad (en vidéo)

• Plus

• p point debrab At free.fr