Présentation rapide de DGPad (en vidéo)
Construire une rosace dynamique par programmation
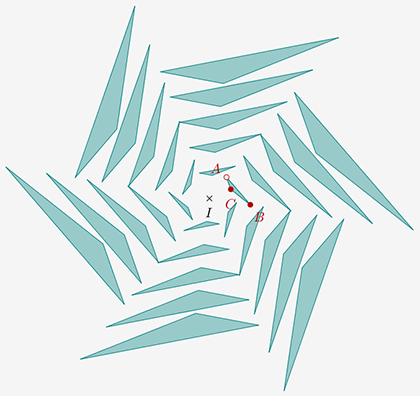
Il n'y a pas que les pavages dans la vie (et dans les programmes du cycle 4 au collège). Il y a aussi les rosaces (dont on voit pointer le bout du nez dans l'exercice 6 du brevet des collèges session juin 2018 en Asie).
Dans cet article, on va construire une rosace dynamique en utilisant différentes méthodes.
Dans l'exercice du brevet cité dans l'introduction, une figure de géométrie dynamique est le prétexte à poser quelques questions sur l'homothétie. Voici cet exercice :
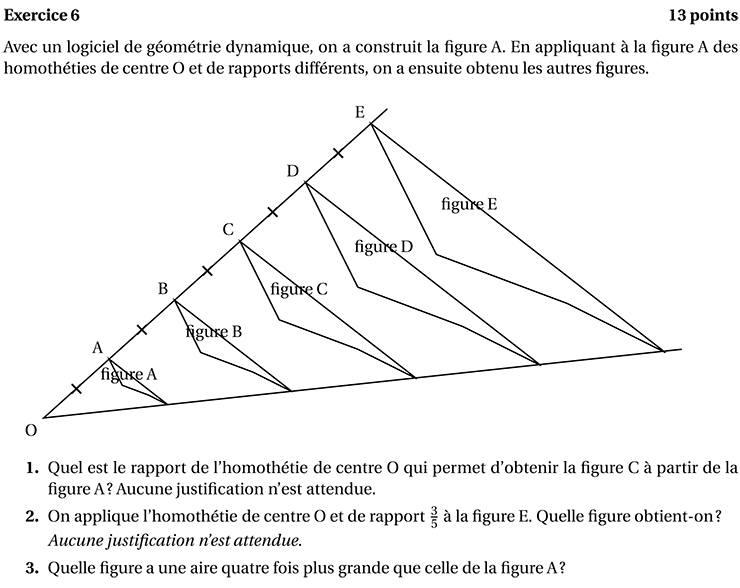
On a le sentiment que le rédacteur était parti pour une rosace mais a été coupé dans son élan.
C'est cette rosace dynamique (en la figure A) que l'on va s'évertuer à construire dans le présent article en utilisant différentes approches (transformations, tortue) et différents logiciels (CaRMetal, DGPad).
En pratique, on va utiliser 3 méthodes :
- des transformations avec CaRMetal
- une tortue dynamique avec CaRMetal
- une tortue dynamique avec DGPad
Remarque : si l'on regarde attentivement, on voit que les figures tracées sont des quadrilatères. Mais on va considérer ici que ce sont des triangles. Foncièrement, cela ne change pas le problème et cela permettra d'avoir un code plus concis.
I) La série de triangles homothétiques
A) Avec des tranformations (CaRMetal)
1) Préliminaires dans l'interface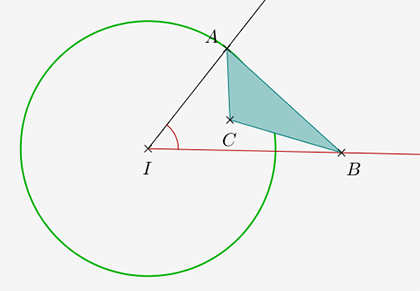
On commence par créer un point I et un cercle de centre I et de rayon 1. (On a appelé le centre I, on pourrait l'appeler O comme dans l'énoncé du BAC).
A est un point sur le cercle. On trace la demi-droite [IA). On masque le cercle.
On trace un angle de mesure donnée libre \(\widehat{AI...}\) et on place B sur le deuxième côté de l'angle.
C est un point libre, que l'on place dans le secteur angulaire.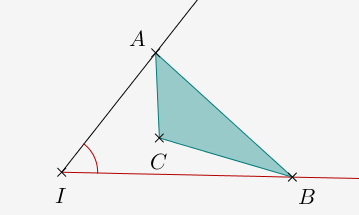
2) On crée un nouveau script.
On commence par pseudo-code pour signifier à l'éditeur que l'on va écrire en pseudo-code.
On coche la case "en français".
Dans cette première approche, on va utiliser la macro homothétie, qui est une macro de menu, comme on peut le voir en déroulant ce menu.
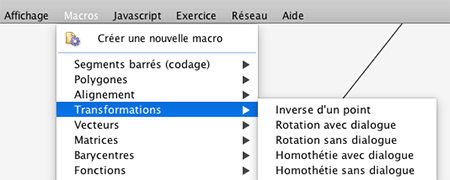
On peut écrire ce script :
On obtient cette figure dynamique :
B) Avec une tortue dynamique (CaRMetal)
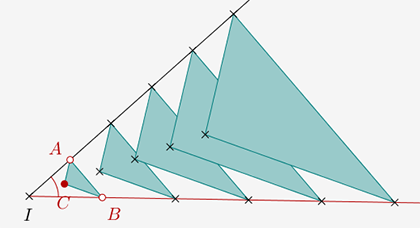
On part de la même figure initiale.
On utilise la tortue dynamique pour réaliser une fonction Javascript qui réalise l'homothétie. Cette fonction remplace l'application de la macro.
Voici le script :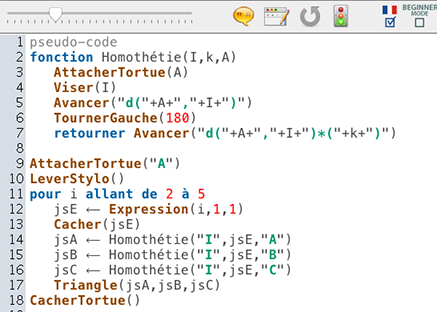
On obtient la même figure dynamique que précédemment :
C) Avec une tortue dynamique (DGPad)
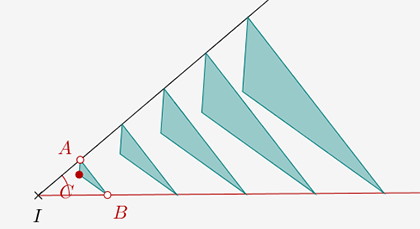
Avec DGPad, on a une tortue dynamique qui construit une trace sous forme d'une série de points et pas à proprement parler des points.
Les triangles doivent être obtenue par remplissage d'une partie de cette trace.
On crée la même figure initiale que pour CaRMetal (via l'interface et ses outils infixés).
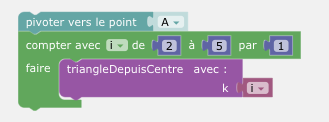
Puis on ouvre l'onglet tortue des propriétés du point I et on pivote vers le point A.
Ensuite, on écrit une fonction (procédure) qui construit un triangle homothétique à ABC :
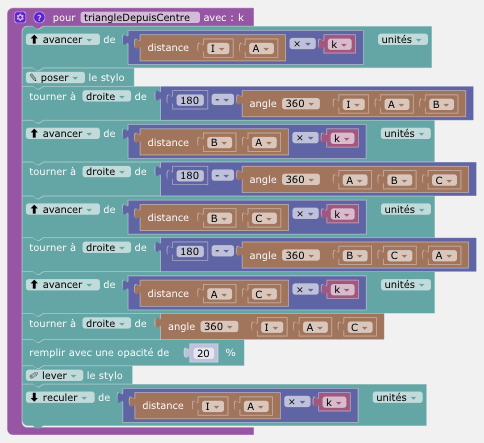
Enfin, on complète le script principal pour obtenir le script suivant :
On obtient cette figure dynamique (l'effet graphique lors du zoom a été obtenu en épinglant les points B et C).
D) Illustration graphique des paradoxes sur les augmentations et réductions en pourcentages.
Cet exercice peut donner l'idée d'une activité pour illustrer graphiquement les paradoxes sur les augmentations et réductions en pourcentages.
On va se placer dans la situation où le triangle est rectangle isocèle et imaginer que chaque triangle (non rempli) constitue une "pièce" de monnaie.
On peut remarquer que l'on est dans une situation de Thalès (avec une homothétie de centre I) et que par conséquent les longueurs AB, BC, CA, IA, IB, IC et le périmètre de ABC sont toutes proportionnelles l'une par rapport à l'autre.
On va faire en sorte que la valeur d'une pièce soit également proportionnelle à toutes ces longueurs et choisir :
La figure A vaut 1 euro, la figure B vaut 2 euros, etc.
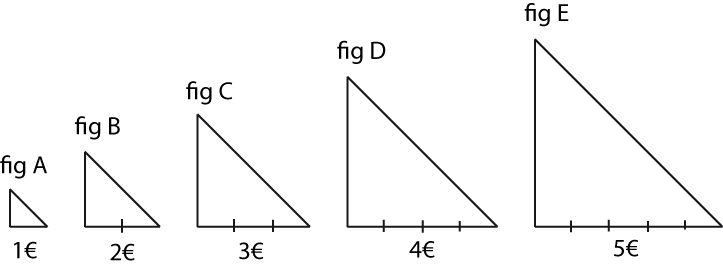
On peut alors traduire les transformations d'un triangle à l'autre par des réductions ou par des augmentations en pourcentages :
On voit bien que "l'inverse" d'une réduction de 50% n'est pas une augmentation de 50% car c'est une augmentation de 100% !
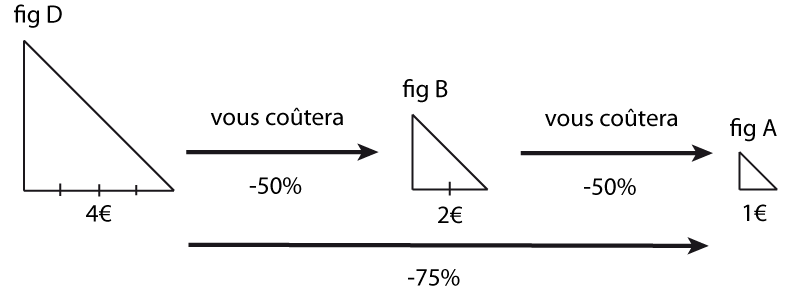
De même, on voit que ce n'est pas "transitif" :
Deux réductions successives de 50% correspondent non pas à une réduction globale de 100%, mais à une réduction globale de 75%.
II) La rosace
A) Avec des tranformations (CaRMetal)
On commence par ajouter un curseur entier n en utilisant l'outil de la palette Contrôles
Puis on fixe la mesure de l'angle a pour qu'elle soit égale à 360/n.
La rosace sera invariante par rotation d'angle 360/n.
Remarque : dans CaRMetal, les boucles ne sont pas dynamiques. La rosace ne sera pas dynamique en n (qui doit être fixé avant l'exécution du script).
Il faut ajouter un niveau de boucle pour les rotations.
Si on choisit d'appliquer la rotation par récurrence contrairement aux homothéties, que l'on applique toujours aux sommets du triangle initial, il vaut mieux insérer la boucle des rotations ( qui "revient à son point initial") dans la boucle des homothéties.
Voici le script :
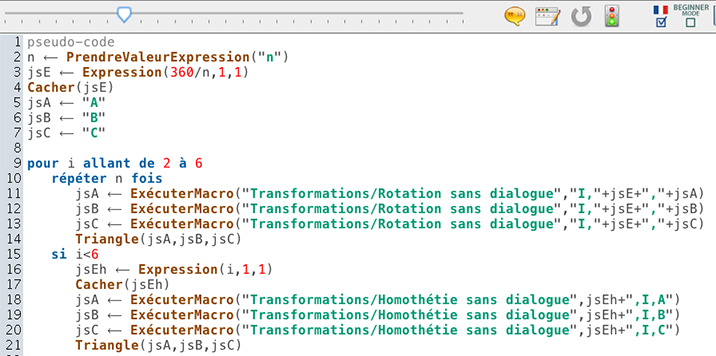
On obtient cette rosace dynamique :
B) Avec une tortue dynamique (CaRMetal)
Avec la tortue, on remplace la rotation par une fonction Javascript qui utilise la tortue. A ceci près, le script est identique :
C) Avec une tortue dynamique (DGPad)
Comme pour CaRMetal, on commence par créer un curseur entier n.
Puis on fixe la mesure de l'angle a pour qu'elle soit égale à 360/n.
La rosace sera invariante par rotation d'angle 360/n et dynamique en n.
La fonction (procédure) triangleDepuisCentre qui construit un triangle homothétique à ABC ne change pas.
Mais cette fonction est appelé dans une double boucle (le triangle initial est tracé deux fois, on pourrait bien-sûr l'éviter).
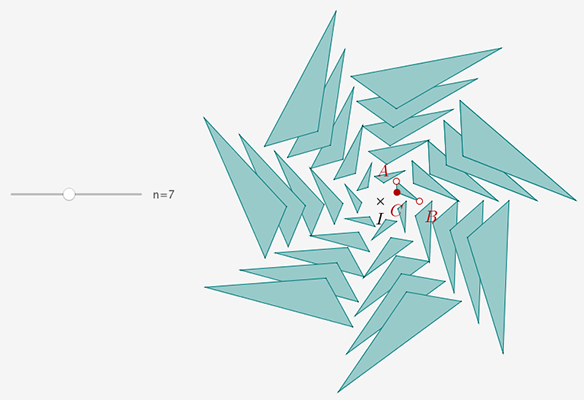
On obtient cette figure dynamique en n (l'effet graphique lors du zoom a été obtenu en épinglant le point C).
Comme souvent avec DGPad, on obtient de très jolies figures en modifiant la valeur du curseur n ou en déplaçant les points libres (ou semi-libres), voire ici en zoomant/dézoomant.
