Représentation graphique des fonctions avec DGPad

Remarques :

• La partie importante de cet article concerne la représentation graphique d'une fonction définie par un algorithme.
• Comme pour CaRMetal, on (= le développeur Eric Hackenholz) a fait le choix de ne pas autoriser le passage à un repère natif qui ne serait pas orthonormé (le passage à ce type de de repère pervertit les outils, l'outil cercle ne produisant plus un cercle, etc). Quand on veut utiliser un repère non orthonormé, la pratique recommandée est de créer un repère flottant (voir la partie 3)).

1) Fonction donnée par sa formule algébrique

A) Formule y = f(x)

On crée une expression (6ème bouton de la barre inférieure) et on lui donne comme valeur la formule.

DGPad reconnaît une expression qui, potentiellement, a une représentation graphique et affiche un bouton permettant de créer cette représentation graphique (en plus de l'expression elle-même). On peut renseigner les bornes min et max si nécessaire.
Si on clique sur ce bouton, on crée l'expression et la représentation graphique.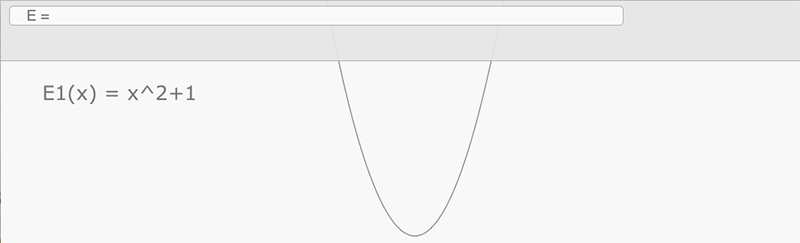

On peut afficher le repère (dernier bouton = interrrupteur de la barre inférieure).

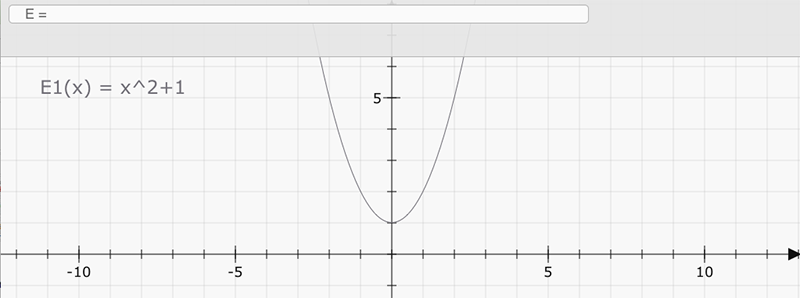
On n'est pas obligé d'utiliser $x$ comme variable. DGPad reconnaîtra de la même façon $y$, $z$ ou $t$.

B) Courbes paramétriques

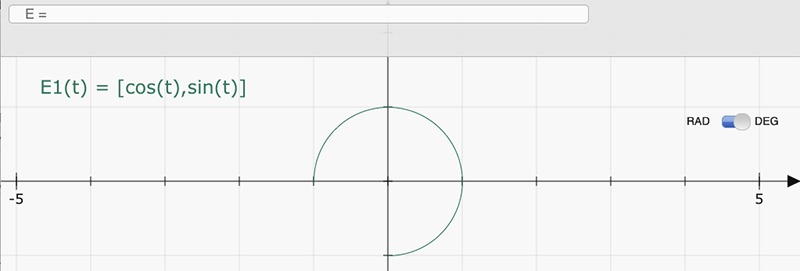
Selon la logique de DGPad, on crée cette fois une expression ayant pour valeur [x(t),y(t)]. Les bornes min et max doivent être renseignées.

C) Plan complexe

L'utilisation du symbole i permet d'entrer une fonction à valeur dans le plan complexe.

2) Fonction définie par un algorithme

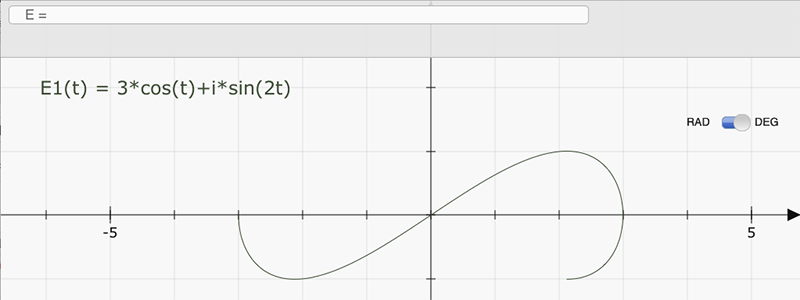
Dans ce cas, il faut construire la courbe par un script qui intègre l'algorithme en question.
DGPad présente l'atout essentiel de pouvoir le faire en programmation dynamique (= en maintenant des liens dynamiques avec des points et des curseurs).

On peut utiliser deux curseurs continus xmin et xmax pour avoir des bornes dynamiques.
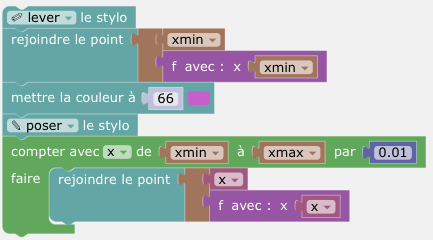
Pour construire la représentatuon graphique, on utilise la tortue dynamique d'un point de la figure (que l'on peut créer si nécessaire, puis masquer).
Le script fait usage de m'instruction rejoindre, qui permet d'exploiter le point de vue repéré avec la tortue. Voici le script général :

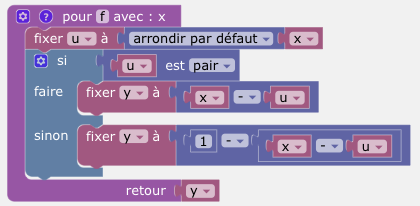
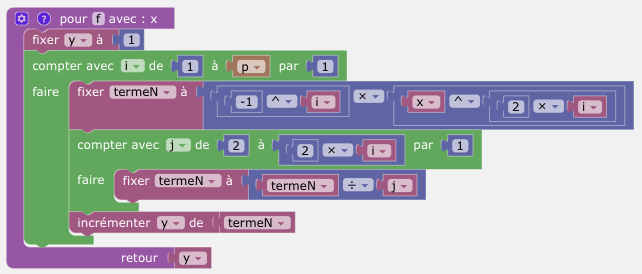
On définit la fonction f par un algorithme.
Par exemple, on peut définir cette fonction f.

On obtient la représentation graphique suivante :

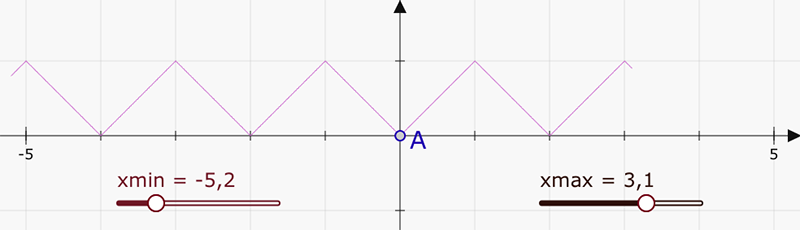
Cette méthode pourra être utile pour représenter des développements de fonctions et illustrer la convergence.

On peut par exemple représenter graphiquement le n-ième développement de Taylor en 0 de la fonction cosinus avec un curseur dynamique entier p. (n=2p)

Le développement de Taylor est $cos(x) \approx 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - ... +(-1)^p \dfrac{x^{2p}}{(2p)!}$

On obtient cette figure dynamique :

3) Représentation graphique dans un repère flottant non orthonormé

Quand on veut utiliser un repère non orthonormé, une bonne pratique consiste à utiliser un repère flottant. En effet, dans ce cas la représentation graphique n'est plus de même nature que les autres objets de l'espace de géométrie dynamique, et il est donc logique de la tracer sur un calque différent.
On peut nommer A le centre du repère orthonormé natif, et on peut alors utiliser trois points libres O,I,J et construire la courbe dans le repère défini par (O,I,J).
On imposera souvent à I d'être sur la parallèle à (Ax) passant par O, et à J d'être sur la parallèle à (Ay) passant par O (repère orthogonal).

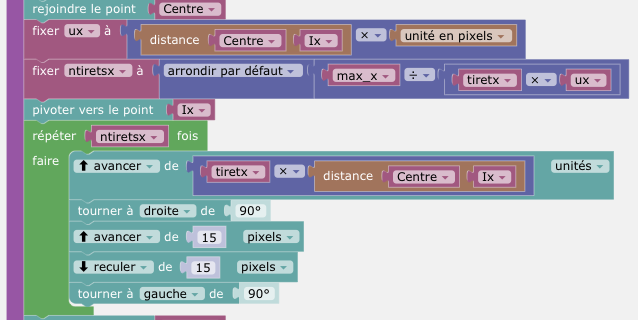
La tortue permet de graduer les axes.
On va proposer un script (des procédures) qui pourra être copié-collé pour s'adapter aux différentes situations. La fonction pourra être choisie librement, on va reprendre ici l'exemple du n-ième développement de Taylor de la fonction cosinus. Certaines variables sont à renseigner dans le script (on a préféré ne pas trop multiplier les curseurs), d'autres par curseurs.

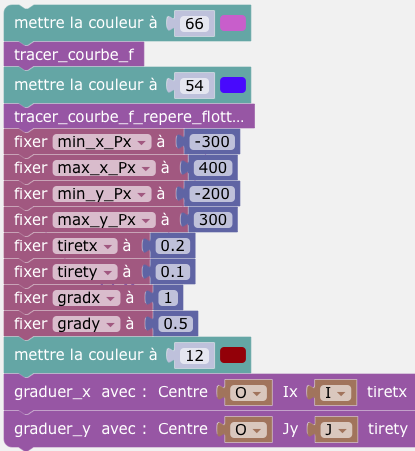
min_x_Px est la valeur min de x en pixels du repère flottant (indépendamment de la courbe de f).
...
tiretx est la distance en unités entre deux tirets sur l'axe horizontal.
...
gradx est la distance en unités entre deux graduations (chiffrées) sur l'axe horizontal.

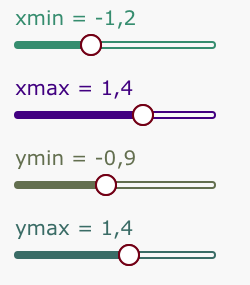
La courbe de f est tracée pour x entre xmin et xmax.
Les axes fléchés (mais pas gradués) suivent les valeurs xmin et xmax, ymin et ymax.
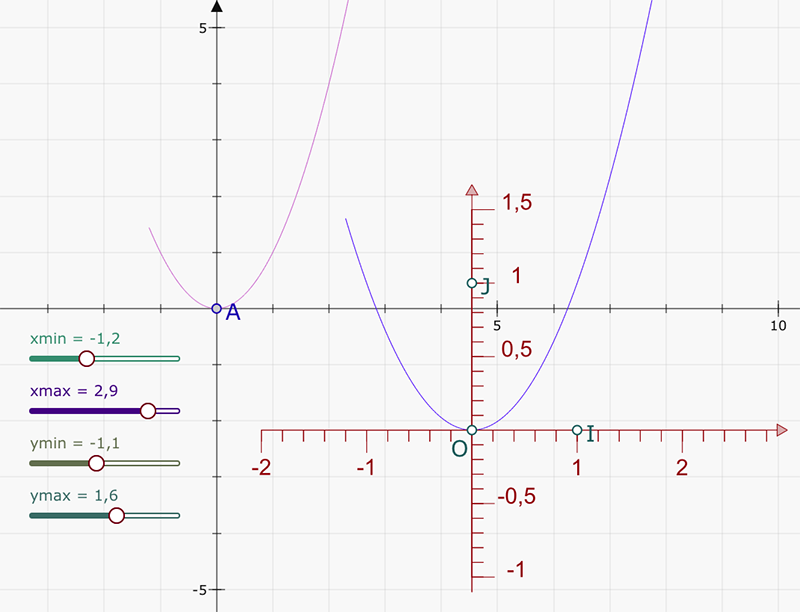
Pour la fonction carrée, on obtient cette courbe (on a représenté la fonction dans le repère natif et dans le repère flottant).

Quelques zoom sur le script :

Tracé de la courbe dans le repère flottant :

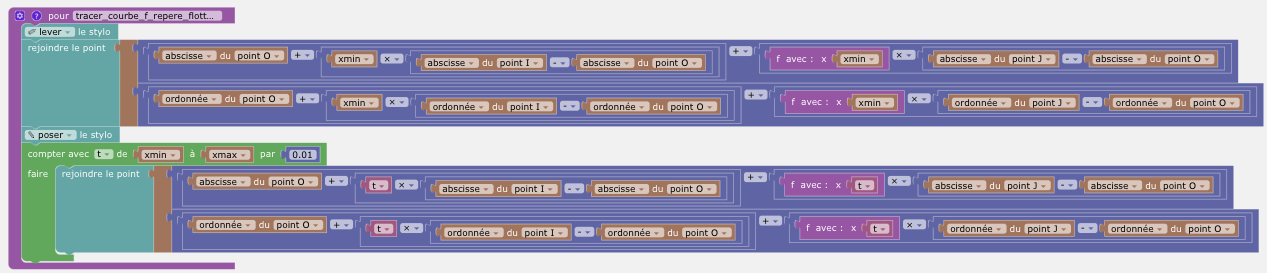
Initialisation et lancement des procédures pour le tracé des axes et leur graduation :

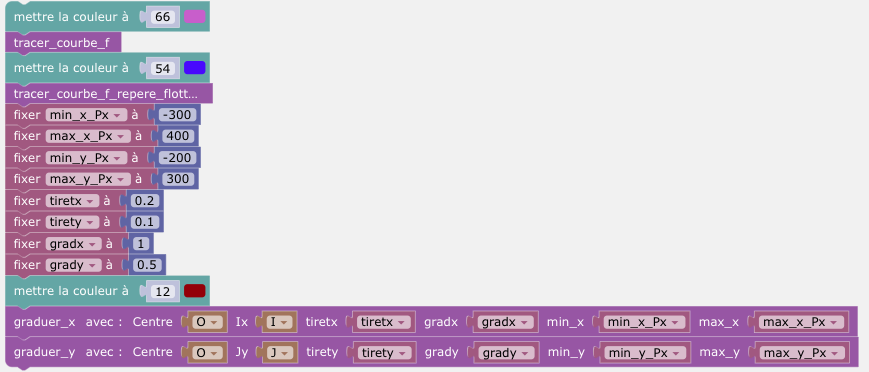
Tracé des axes:

Début de la graduation de l'axe horizontal :

Et pour finir voici la figure dynamique (tout le code tortue est en A) pour le n-ième polynome de Taylor de la fonction cos.

Pièces jointes :

repere_flottant_01.dgp [Repère flottant avec fonction carrée(code tortue en A)]

repere_flottant_Taylor.dgp [Repère flottant avec développement de Taylor de cos(code tortue en A)]