Présentation rapide de DGPad (en vidéo)
Variation autour du pavage de Diane (BAC STD2A Antilles-Guyane - juin 2018)
Le sujet du BAC STD2A Antilles-Guyane de juin 2018 est un sujet très inspirant. (Merci à son concepteur inconnu!)
On va s'intéresser ici à l'exercice 3, qui se terminait par la construction d'un pavage assez "inattendu" et du plus bel effet !!!
...? ;)...
A) Avec CaRMetal
1) Construction du carreau
Contrairement au sujet initial, on ne va pas utiliser les coordonnées (ce qui permettra d'obtenir des figures dynamiques en O et B).
On crée deux points O et B libres.
On crée un angle de mesure donnée égale à 60°.
On crée un cercle de rayon donné de centre O et de rayon d(O;B)/2
On place le point D à l'intersection du côté de l'angle et du cercle.
On crée le point C en utilisant l'outil translation de la palette construction.
Puis on masque le cercle et l'angle et on construit le parallèlogramme.
Les préférences pour les polygones s'appliquent:
On obtient cette figure, dynamique en O et B :
2) Construction du motif
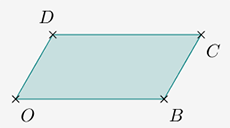
On souhaite maintenant construire l’image du parallélogramme OBCD par la rotation de centre O, d’angle 60° et de sens anti-horaire.
On peut le faire via l'interface en utilisant la macro Rotation sans dialogue.
On commence par créer une expression a60 ègale à 60 pour disposer de l'angle sous forme d'un objet de CaRMetal.
Ensuite on applique la macro de menu.
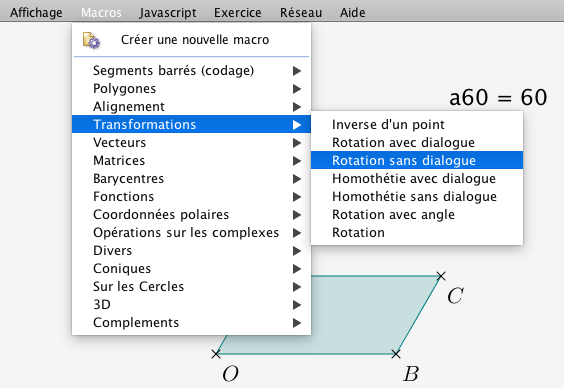
Preview au survol :
image du parallélogramme par rotation :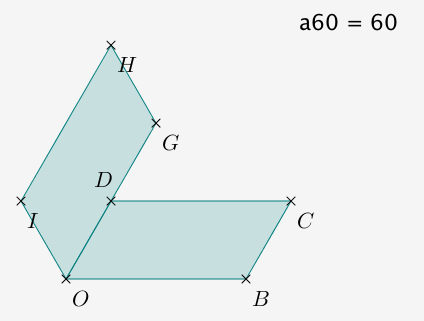
On va maintenant créer le motif entier à partir du seul parallélogramme OBCD (l'expression a60 sera créée par script).
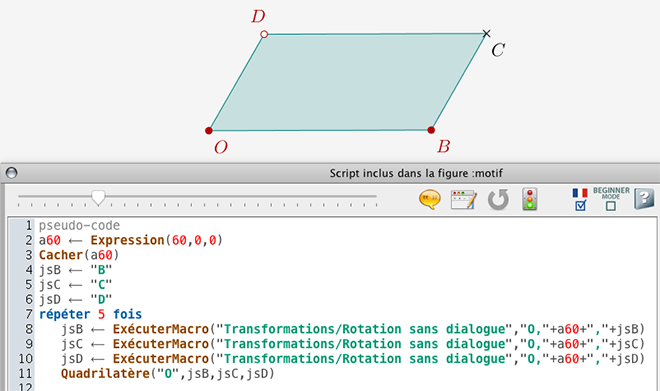
On exécute le script et on obtient le motif :
Si on choisit ces préférences pour ces points (ce que l'on fera désormais) :
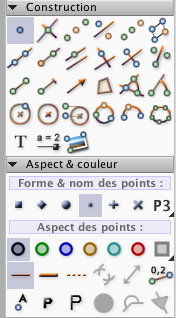
... on obtient cette figure :
3) Construction du pavage
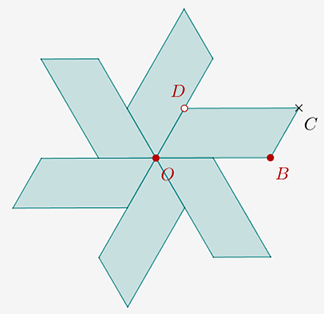
On part de la figure suivante. Le parallélogramme initial a été supprimé et on a créé les points E et F.
La droite (AB) a été construite pour pouvoir utiliser l'outil symétrie axiale.
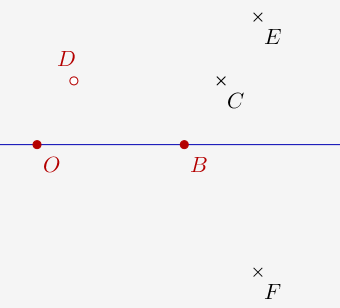
Le pavage peut être obtenu par translations de vecteurs \(\vec{OE}\) et \(\vec{OF}\)
On masque tout sauf les points O et B
Dans le script pour construire le pavage, on utilise une double-boucle. Les variables j2... permettent de retenir la position du premier parallélogramme de la ligne. C'est ce parallélogramme qui subit la translation de vecteur \(\vec{OE}\), les autres la subissent par procuration.
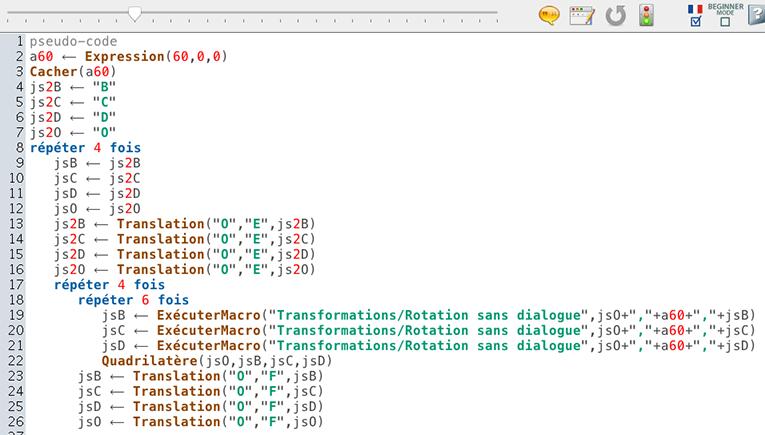
On obtient ce pavage :
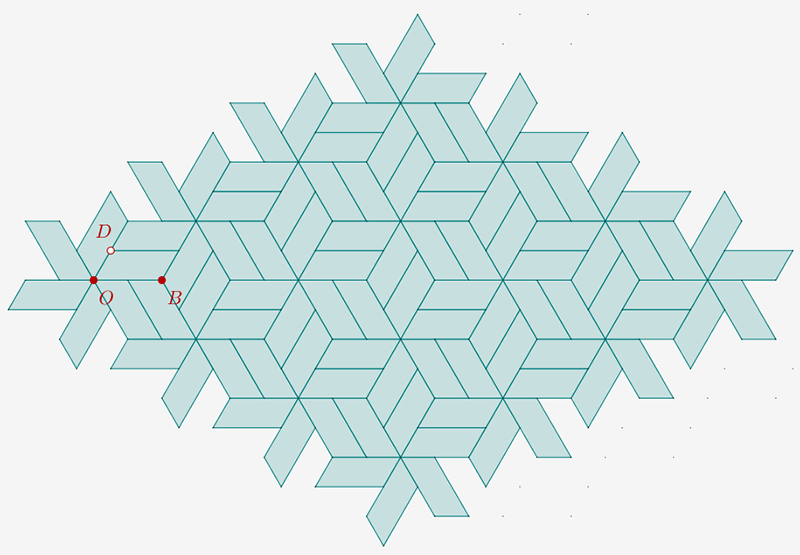
Si on veut se débarasser de points type "moucheron" choisir come préférence pour les points un "coutour pointillé" (ce qui aura pour effet de rendre invisibles tous les points créés par le script).
3) Construction du pavage bicolore
Dans le script, on doit juste construire le milieu du segment [OB] et les triangles correspondants plutôt que le quadrilatère. Et on doit contrôler leur couleur.
On obtient une variante du pavage de Diane.
Avec un choix de préférences différentes pour les points ("contour pointillé" autrement dit invisible) et les polygones ("contour pointillé" et opaque), on obtient cete version :
3) Construction du pavage bicolore à l'aide d'un arbre de Pythagore
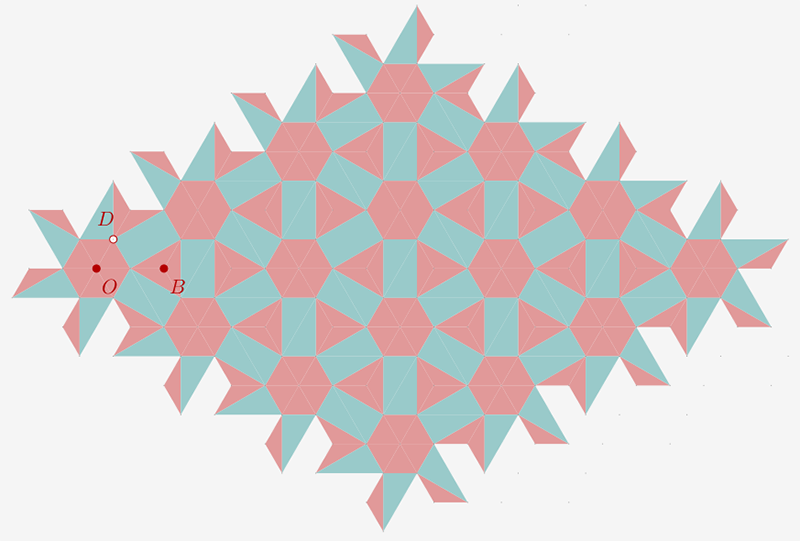
Comme le pavage de Diane, ce pavage peut être obtenu par un "arbre de Pythagore" avec un triangle équilatéral.
On va le faire ici par récursivité avec la méthode par macro de CaRMetal (méthode très claire et efficace).
1) Création de la macro à plusieurs finaux
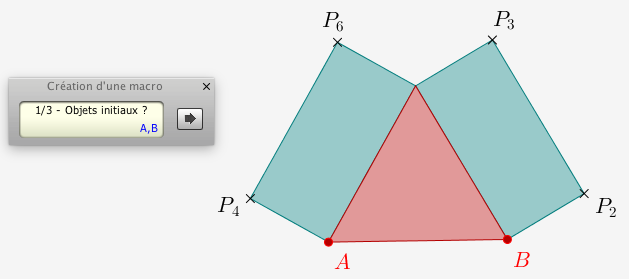
On part de deux points libres A et B et on construit une étape de l'arbre :
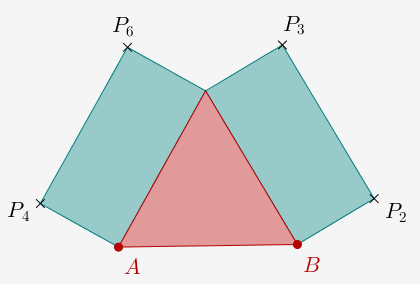
Le nom des points est indifférent.
\(BP_2 = AP_4=AB/2\)
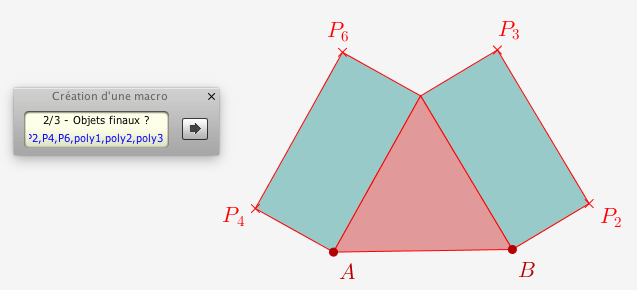
On construit la macro dont les initiaux sont A et B, et dont les finaux sont (retenir l'ordre pour l'application de la CaRCommande ExécuterMacroCommeDéfinie) \(P_3\), \(P_2\), \(P_4\), \(P_6\), poly1, poly2, poly3
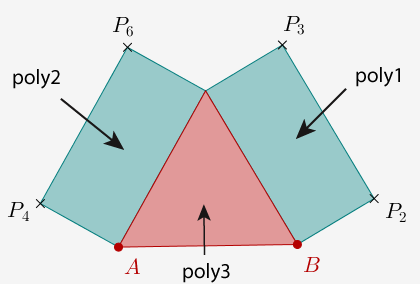
En détail :
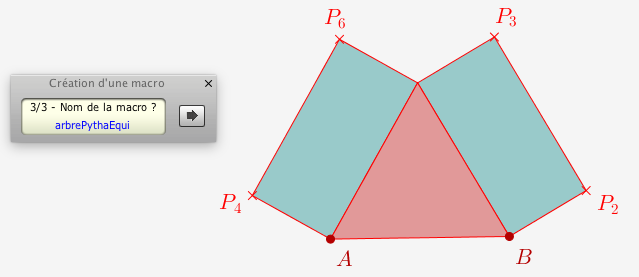
On dispose alors d'une nouvelle macro de menu et on peut tout effacer (menu Edition/Effacer tout).
On recrée les points libres A et B.
La macro arbrePythaEqui est visible dans le menu des macros.
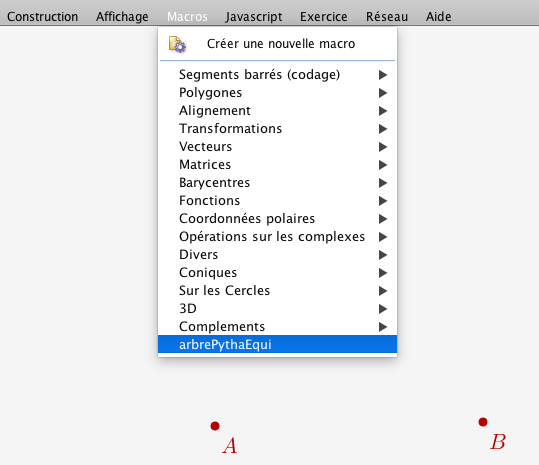
On peut tester cette macro sur les points A et B (preview dans l'illustration ci-dessous) :
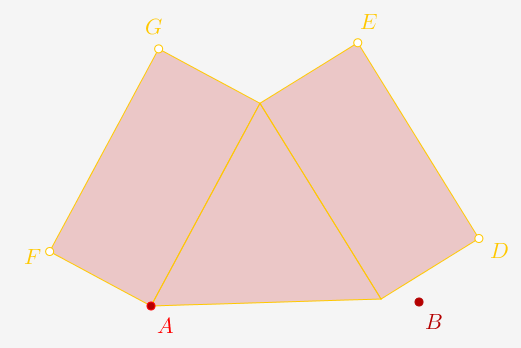
2) Programmation d'une fonction récursive pour construire l'arbre de Pythagore
On utilise la CaRComande ExécuterMacroCommeDéfinie avec l'ordre des finaux choisis lors de la création de la macro (ou, pour les étourdis, on ouvre le panneau de gauche des macros puis clic droit sur la macro et lien de menu Montrer les propriétés)
On crée un nouveau script :
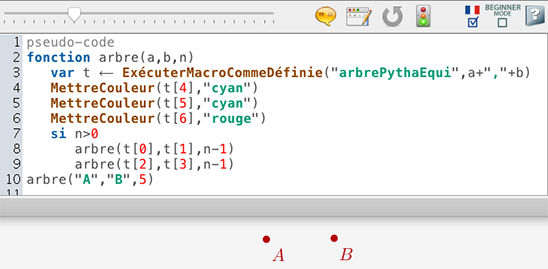
Le script est réduit à son strict minimum.
Comme préférences, on fixe :
* pour les points : une forme "point" et un "contour pointillé", ce qui aura pour effet de masquer les points
* pour les polygones : rempli, "contour normal", "opaque" (pour gérer les superpositions)
L'exécution du script donne le pavage suivant, dynamique en A et B:
A) Avec DGPad (tortue dynamique)
On va le faire ici de façon très méthodique en programmant des procédures tortue qui tracent un motif et font revenir la tortue à sa position initiale (c'est la méthode que l'on recommande).
1) Procédure pour le parallelogramme
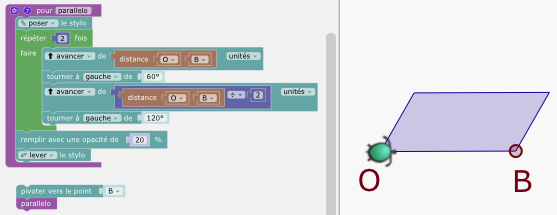
2) Procédure pour le motif
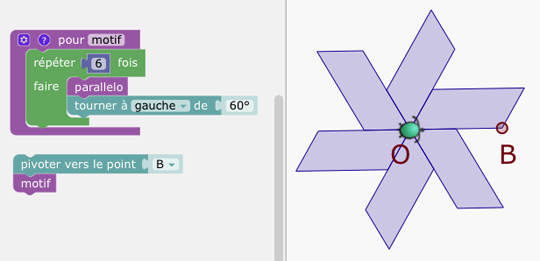
3) Procédure pour la ligne
4) Procédure pour le pavage (sans retour à la position initiale)
Pour obtenir le pavage bicolore, il suffit de changer la procédure pour tracer le parallélogramme
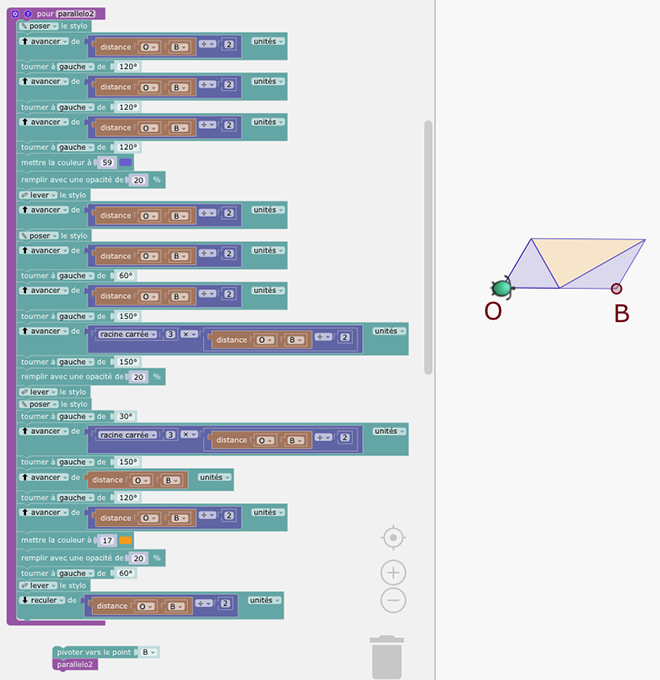
On obtient ce pavage:
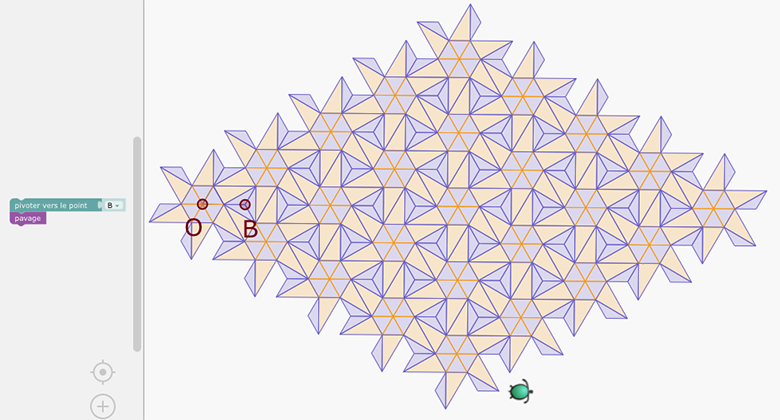
Et pour finir la figure dynamique en ligne, grand bonheur de DGPad :
Avec DGPad (c'est un atout par rapport à CaRMetal) on pourrait ajouter des curseurs dynamiques pour le nombre de motifs posés, mais ce n'est pas le propos ici.
On va terminer en donnant une variante de code assez étonnante pour le pavage bicolore. Celle-ci m'a été suggérée par Yves Martin et mobilise l'instruction tortue rejoindre ainsi que des opérateurs affines sur les points.
Cette variante ne concerne que le code de la procédure parallelo.
On commence par créer une procédure triangle qui trace un triangle rempli à partir de trois points :
On notera qu'à l'issue de cette procédure, compte tenu du fonctionnement de l'instruction rejoindre, la tortue est orientée de P3 à P1.
On crée via l'interface quatre variable O, B, C, D, E qui vont jouer le rôle que leur nom indique. (E est le milieu de [OB])
Ensuite, et c'est là que ça devient étonnant, dans la procédure parallelo2bis, on on affecte à O, B et D des positions de tortue, et à C et E des positions calculées.
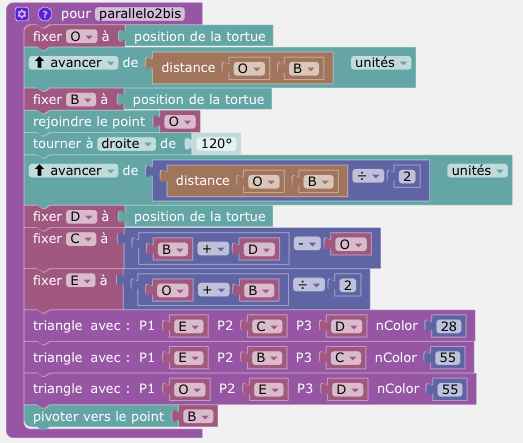
Cette façon de programmer peut sembler (est) très déroutante. Elle illustre que la tortue de DGPad possède des fonctionnalités qui la rendent presque "mutante" (ce concept est présenté dans cet article MathémaTICE).
Et ça marche!
Remarque : le pavage régulier obtenu est de type "héxagonal totalement symétrique", nommé p6m selon la dénomination des cristallographes et M6 selon la dénomination du Kangourou.
