Présentation rapide de DGPad (en vidéo)
Un pavage de l'Alhambra : pavage dynamique avec un motif complexe (01) (BAC STD2A Métropole / LR - juin 2018)
Dans cet article, on va créer une version dynamique d'un pavage visible sur les murs du palais de l'Alhambra.
Ce pavage faisait l'objet de l'exercice 3 du BAC STD2A Métropole - La Réunion de juin 2018
Comme dans le sujet du Baccalauréat (une méthode différente sera présentée à la fin de l'article), on va construire ce pavage de deux façons, en positif et en négatif. Ce pavage sera dynamique en trois points. (On présentera une méthode plus simple en fin d'article.)
On va le construire avec une méthode très simple, en utilisant les outils de l'interface et la CaRCommande ExécuterMacro dans un script.
Le script sera très proche de celui présenté dans les articles précédents présentant un pavage (par la méthode utilisant les translations), à ceci près que le motif, qui est compliqué, sera construit par macro. Autrement dit, on aura des points pilotes (les deux points libres et le point semi-libre) que l'on déplacera par translation avant de leur appliquer la macro créant le motif.
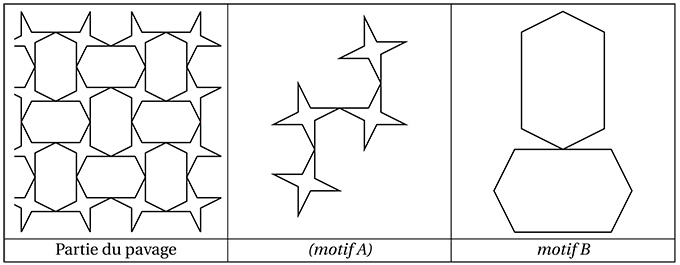
Remarque : ce pavage est un pavage périodique du plan. Il existe 17 types de pavages périodiques (invariants par deux translations indépendantes) du plan. Le pavage présenté est de type "rectangulaire bisymétrique" (ce type est nommé pmm selon la dénomination des cristallographes et M2 selon la dénomination du Kangourou).
En s'écartant de l'énoncé, on pourrait construire le pavage différemment, en appliquant des symétries axiales successives à un motif constitué par une étoile.
I) Création du pavage en positif
Dans ce cas, le motif est constitué par des étoiles. On va considérer, comme dans le sujet du BAC, que le motif comporte 4 étoiles.
La "finesse" des étoiles sera dynamique.
On commence par construire deux points A et B libres, puis un point C sur le cercle de centre A passant par B.
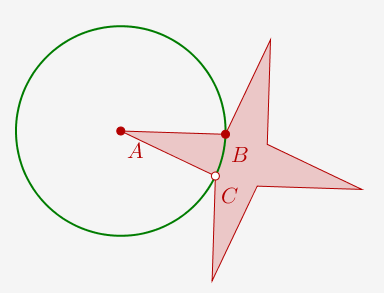
Ensuite, on termine l'étoile :
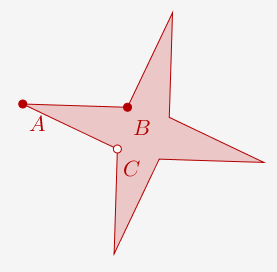
Il y a plusieurs méthodes possibles. Voici par exemple nos traits de construction :
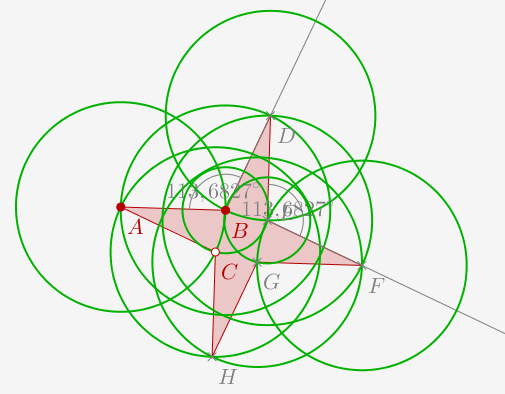
On voit que l'on a utilisé l'outil cercle passant par un point et l'outil angle de mesure donnée.
Ensuite, on crée une première macro nommée une-etoile avec pour initiaux A, B, C et pour seul final l'étoile(polygone).
On poursuit ensuite la construction pour obtenir les points nommés I et K sur l'illustration ci-dessous. (On a construit une droite pour pouvoir utilsier l'outil symétie axiale).
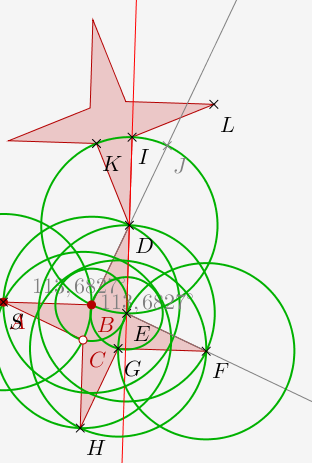
On peut alors appliquer la macro une-etoile à D, K, I.
Puis on peut obtenir les deux étoiles de gauche directement par translation de vecteur $\vec{LA}$ appliquée aux polygones.
On peut alors créer une macro nommée quatre-etoiles avec pour initiaux A, B, C et pour finaux les quatre étoiles.
Le script pour le pavage est alors très simple.
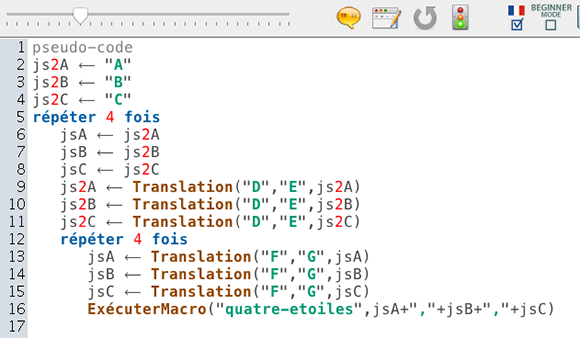
On peut changer le fond et modifier les préférences pour obtenir ce pavage :
II) Création du pavage en négatif
On fait pareil avec les deux hexagones.
Plus précisément, on crée les trois points A, B, C puis on termine l'hexagone et on crée la macro un-hexagone d'initiaux A, B, C et de final l'hexagone.
Ensuite on crée les points G, H, I
Voici nos traits de construction :
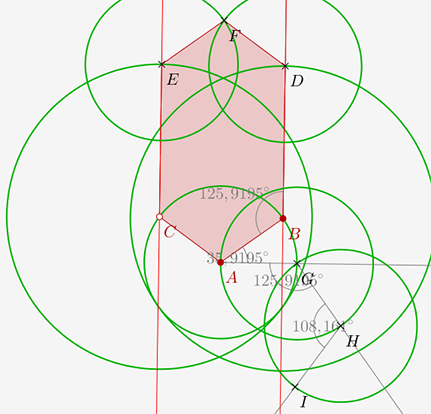
On applique la macro un-hexagone à H, G , I :
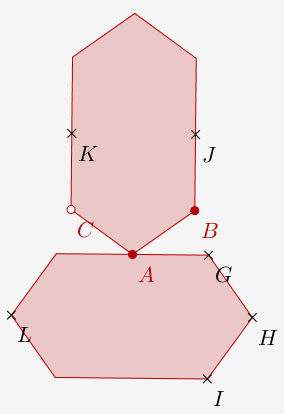
Puis on crée la macro deux-hexagones d'initiaux A, B, C et de finaux les deux hexagones.
On change le fond et on part des trois points A, B, C.
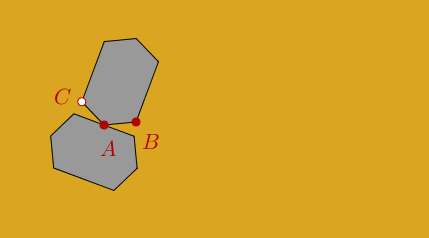
Voici le script, quasi-identique au précédent.
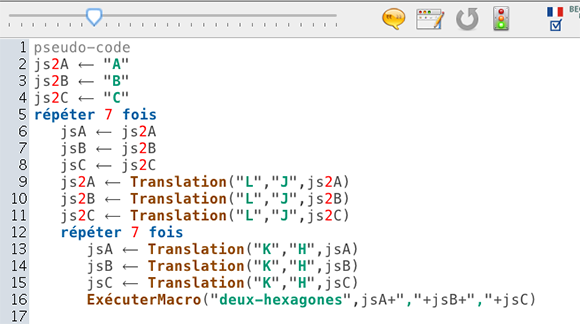
On veille à avoir des préférences cohérentes et on lance le script.
On obtient ce pavage :
III) Méthode différente à partir du "motif minimal"
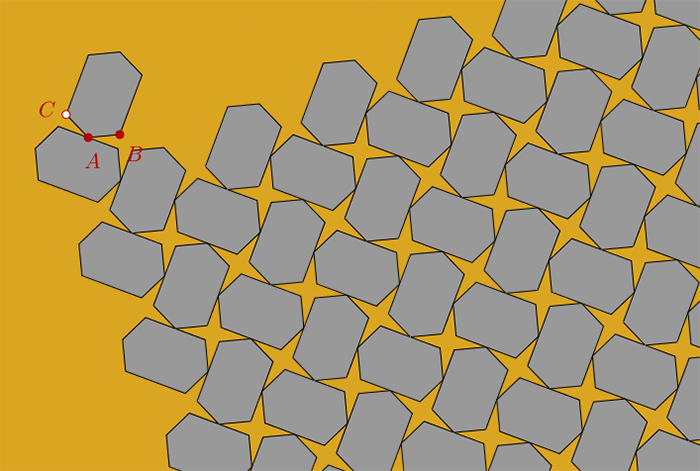
On part d'une étoile et on applique des symétries axiales successives. Pour obtenir un développement en spirale, on peut utiliser le script suivant :
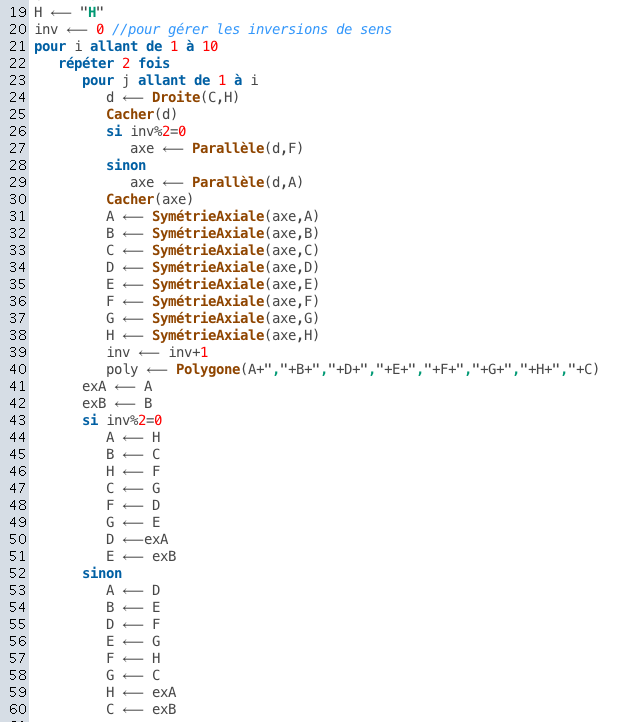
Voir pavage-Alambra-methode-elementaire-pseudo-code.zir
