Présentation rapide de DGPad (en vidéo)
Angles inscrits - CaRMetal - tortue - 2nde
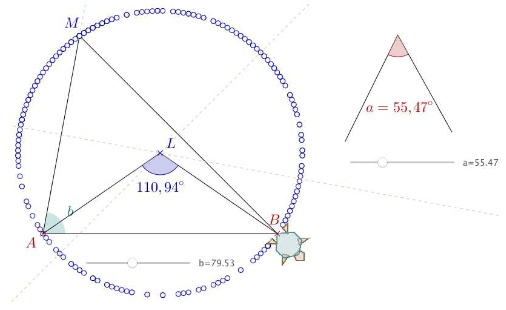
Exercice 1: découverte de la propriété des angles inscrits dans un cercle
Faire apparaître sous forme d'une trace le lieu des points qui voient un segment [AB] sous un angle a fixé.
La trace sera laissée par un point M construit à l'aide de la tortue. Ce point M variera en fonction de l'angle \(\widehat{BAM}\) dont la mesure sera pilotable par curseur. On exploitera la "formule des sinus" (supposée acquise) : \(\dfrac{sin \widehat{A}}{a}=\dfrac{sin \widehat{B}}{b}=\dfrac{sin \widehat{C}}{c}\)
On part de la figure suivante, donnée en p-j (curseurs et angles de mesure fixée par ces curseurs).
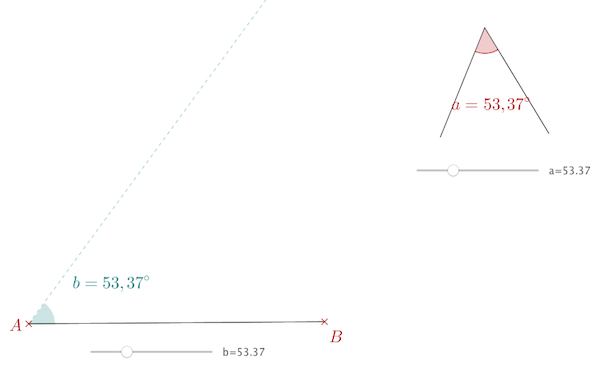
On attache la tortue au point A, on tourne à gauche de b, on avance de \(AB \times \dfrac{sin(180-a-b)}{sin(a)}\) et on arrive au point M.
Ensuite on fait varier le curseur b pour faire apparaître la trace de M.
Exercice 2: compléter via l'interface la figure obtenue par le script précédent pour ajouter le centre L du cercle, puis faire apparaître la mesure de l'angle au centre \(\widehat{ALB}\).
