Présentation rapide de DGPad (en vidéo)
Fractale du Bibendum et fractale beurk!
NB : les scripts présentés dans cet article nécessitent CaRMetal version \(\geqslant\) 4.2.9
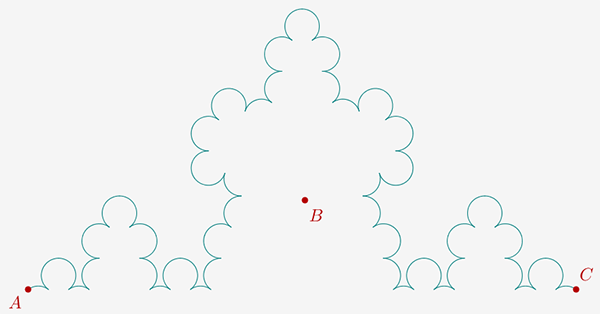
fractale du Bibendum
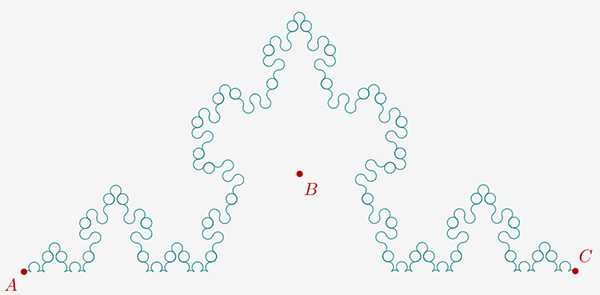
fractale beurk!
Comment construire ces fractales?
La méthode consiste à construire une macro que l'on appliquera récursivement.
On part de trois points libres A, B, C et (dans l'esprit) on transforme l'arc de cercle passant A, B, C. Voici la construction qui permet de construire la macro :
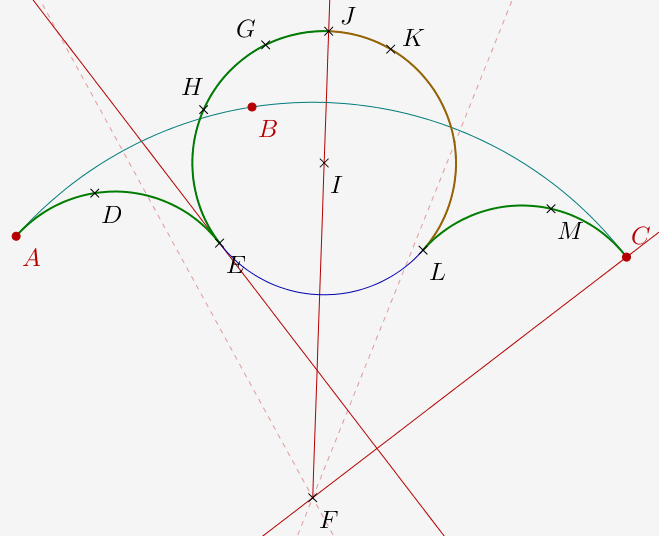
Les points D et E sont obtenus par application de l'homothétie de centre A et de rapport 1/3 (macro de menu homothétie avec dialogue).
Les points L et M sont obtenus par application de l'homothétie de centre C et de rapport 1/3 (macro de menu homothétie avec dialogue).
F est le centre de l'arc de cercle. Il est obtenu comme intersection des médiatrices de [AB] et [BC].
On crée la perpendiculaire à (FC) passant par E, puis les symétriques H et G de D et A par rapport à cette droite.
On construit le cercle circonscrit à E, G, H et son centre I.
On peut alors construire le point J , la droite (FJ) et le symétrique K de G par rapport à (FJ).
On crée une macro reducBulle d'initiaux A, B, C et de finaux D, E, G, J , K, L, M.
On peut alors tout supprimer (la macro est conservée) et repartir d'une figure élémentaire constituée de trois points libres A, B, C.
On crée un nouveau script :
On obtient la fractale du Bibendum.
Si on autorise les arcs rentrants (ligne 5), on obtient la fractale beurk!
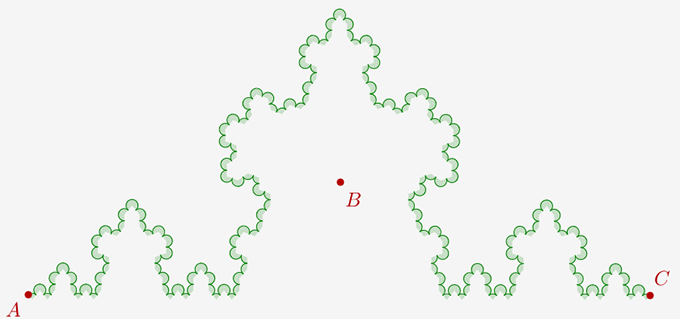
fractale du Bibendum avec l'aspect par défaut "rempli" pour les arcs
Pièces jointes :
fractale du Bibendum [figure CaRMetal avec script]
