
Présentation rapide de DGPad (en vidéo)
NB : les scripts présentés dans cet article nécessitent CaRMetal version \(\geqslant\) 4.2.9
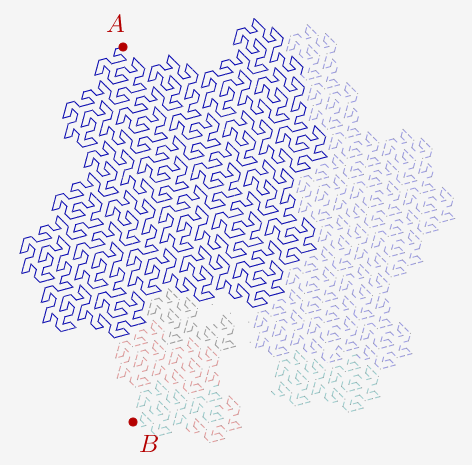
La courbe de Gosper est une courbe de Peano qui couvre le plan.
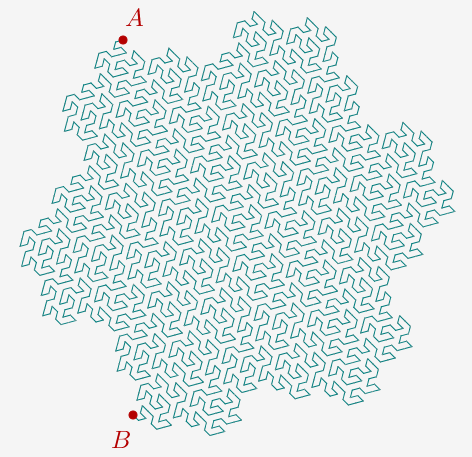
C'est une courbe fractale. On va la construire par récursivité et macro (cette macro étant définie en utilisant la géométrie de la tortue).
Voici le schéma de la construction de la courbe de Gosper :
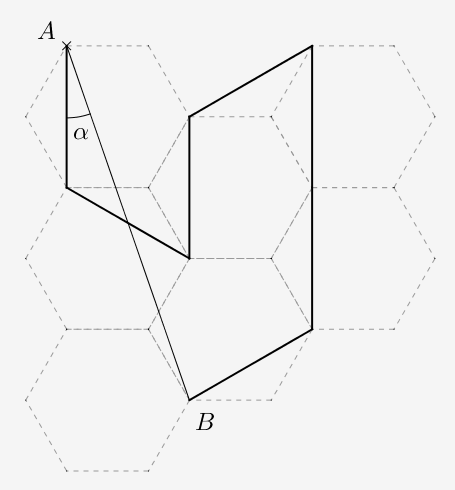
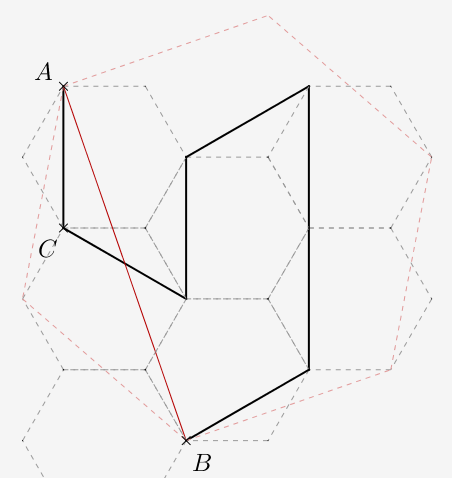
On part d'un sommet d'un hexagone, et on parcourt "de facon identique" les sept hexagones d'un réseau. Ce qui permet de réitérer récursivement le procédé.
On note que l'orientation des hexagones du réseau le long du parcours de A à B change : la partie de plus grande aire est tantôt main droite tantôt main gauche.
Des calculs de trigonmétrie élémentaire permettent de démontrer que \(AB = \sqrt{7} \times AC\) et que \(tan(\alpha)=\dfrac{\sqrt{3}}{5}\)
A chaque itération, on remplace un segment par 7 segments \(\sqrt{7}\) fois plus petit. La dimension fractale de la courbe de Gosper est \(-\dfrac{ln(7)}{ln(\dfrac{1}{\sqrt{7}})}=\dfrac{ln(7)}{ln(\sqrt{7})}=2\). Cette courbe pave le plan. L'ensemble rempli par la courbe est appelé l'île de Gosper.
On va construire une courbe de Gosper dynamique en A, B.
On commence par construire la courbe de Gosper allant de A à B après une itération, ce qui est une formalité en géométrie de la tortue.
On crée un script intitulé pourMacroGosper

On lance ce script et on obtient cette figure.
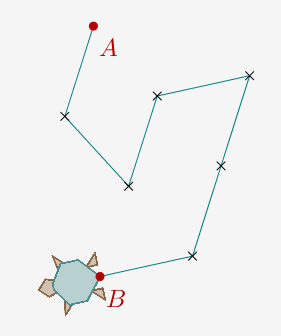
On peut alors construire la macro gosper d'initiaux A, B et de finaux les sommets de la ligne brisée (dans l'ordre).
Il ne reste plus qu'à appliquer récursivement la macro pour obtenir la courbe de Gosper.
On crée un nouveau script.

Il faut être attentif à l'orientation.
On choisit l'aspect par défaut pour les points et pour les segments avant de lancer le script.
On obtient la courbe de Gosper (à une étape donnée) dynamique en A, B.
courbe_Gosper.zir [figure CaRMetal avec script]