Présentation rapide de DGPad (en vidéo)
Variations autour de l'épreuve de maths du bac S Métropole–La Réunion juin 2018
Dans cet article, on va "corriger" le sujet du Bac S donné en Métropole session juin 2018 avec CaRMetal et DGPad en illustrant graphiquement différentes parties.
Exercice 1
On peut tracer la chaînette avec DGPad en utilisant son équation :
- On crée une nouvelle expression égale à (exp(x)+exp(-x)-2)/2
- DGPad reconnaît une formule de fonction et donne la possibilité de tracer sa courbe. On valide en appuyant sur le bouton correspondant.
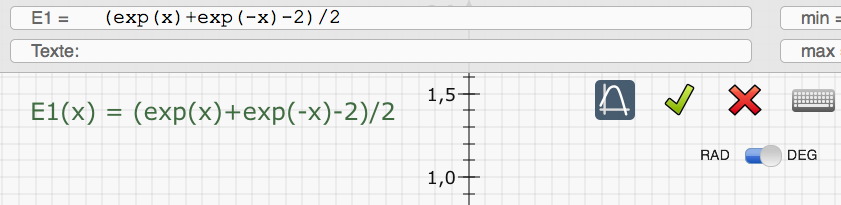
On obtient la courbe de la chaînette.
Question 5.
On peut programmer l'algorithme de dichotomie en pseudo-code avec CaRMetal :
\(2,5 -2,4375 = 0,0625=\dfrac{1}{16}=(\dfrac{1}{2})^{4}\). Le résultat est obtenu après 4 étapes, ce qui était prévisible.
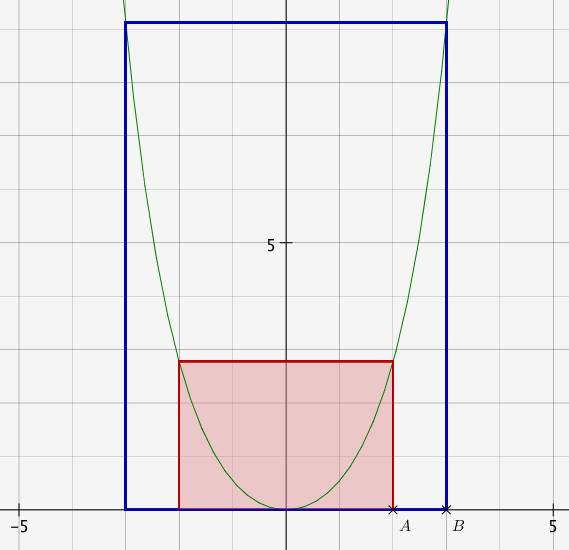
On peut illustrer graphiquement la convergence des rectangles pour x = a et pour x = b vers un carré.
On commence par construire la chaînette avec l'outil de l'interface.
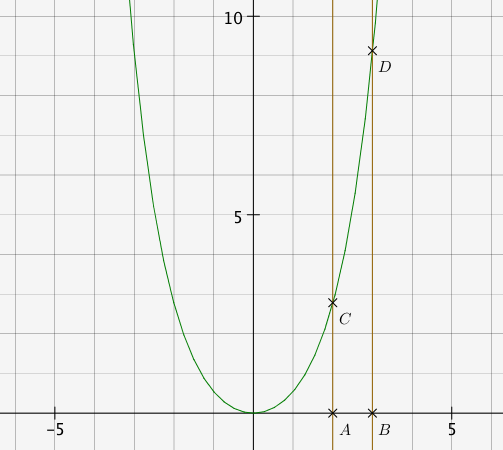
On construit ensuite les points A(2;0) et B(3;0), les paralléles à (Oy) passant par A et B, puis les points d'intersection C et D.
On peut ensuite masquer les droites et construire les rectangles.
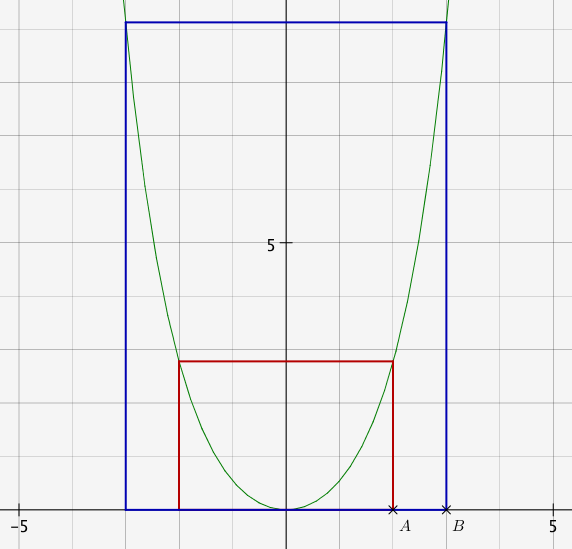
On peaufine la figure en activant la trace des côtés des deux rectangles, et en traçant le rectangle rouge (polygone).
Enfin, on reprend le script en pseudo-code et on l'adapte légérement.
En demandant une précision égale à 0,01 on obtient cette figure :
Exercice 3
Pour étudier les triangles orthocentriques avec CaRMetal on peut commencer par créer un tétraèdre régulier avec l'outil de l'interface, puis libérer les sommets.
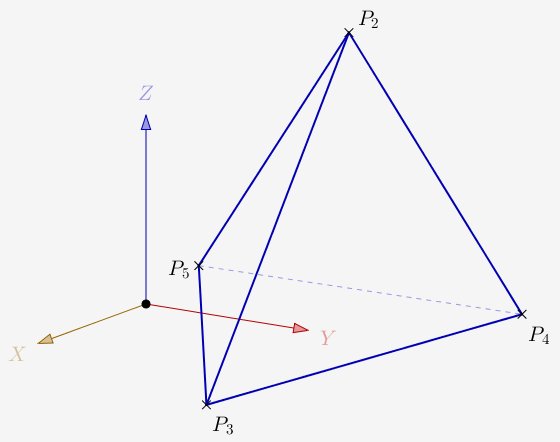
Puis on peut créer les hauteurs avec l'outil projection sur un plan.
On crée ensuite un cube, toujours avec un outil de l'interface, et on pourra fixer temporairement les sommets du tétraèdre sur certains sommets du cube.
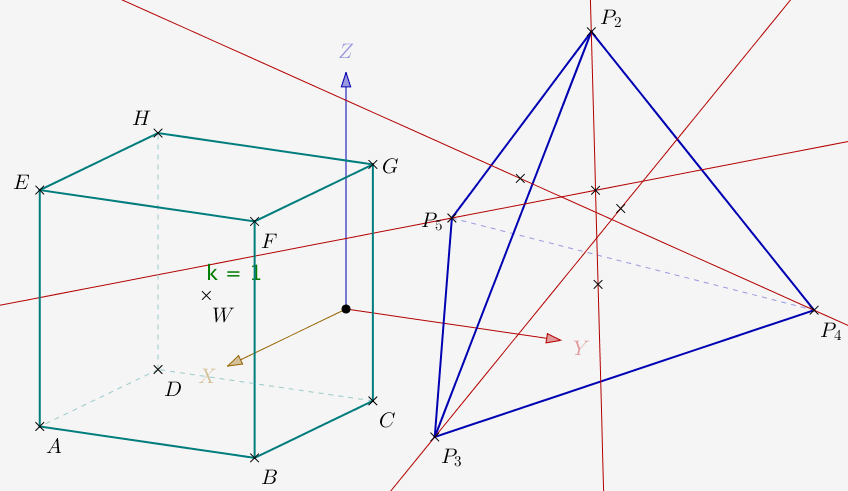
On peut fixer les points par un script. Pour le tétraèdre ABCE :
On obtient cette figure :
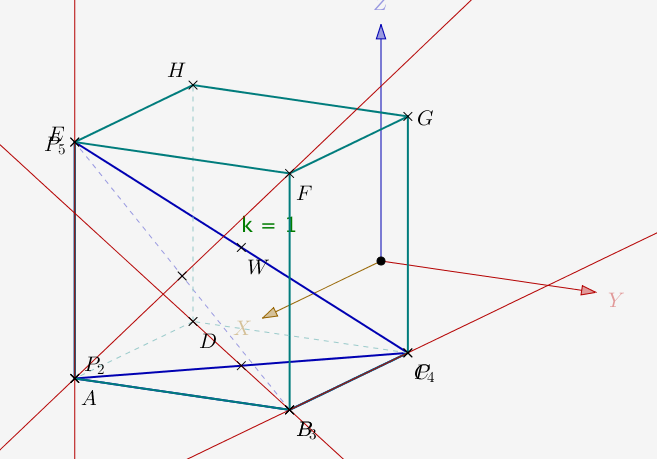
On constate que dans ce cas les hauteurs ne sont pas concourantes.
Pour le tétraèdre ACHF :
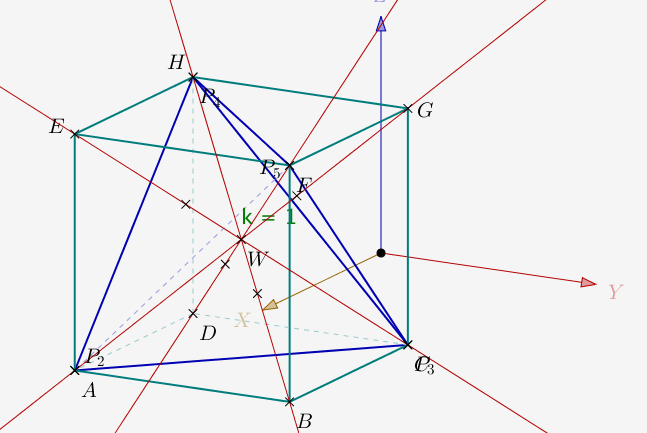
On constate que dans ce cas les hauteurs sont concourantes.
Enfin, pour le tétrèdre RSTU :
On obtient cette figure
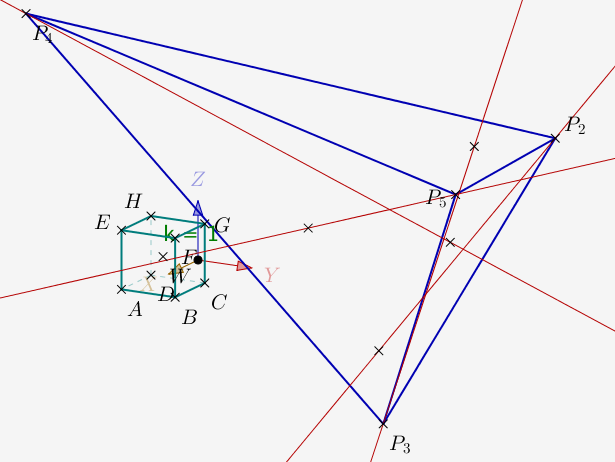
On constate que les hauteurs de RSTU ne sont pas concourantes.
Exercice 4
Pour afficher la ligne brisée, on crée un point A, puis le script tortue du point A.
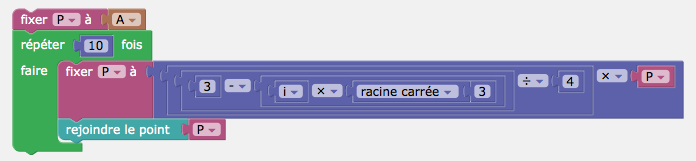
On obtient cette figure dynamique:
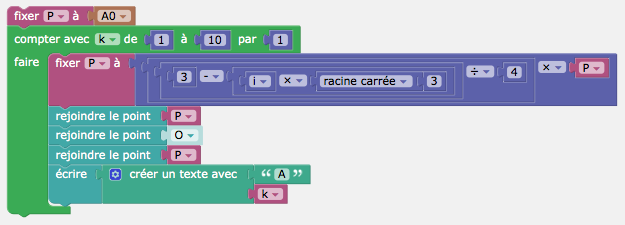
Pour afficher le nom des points, on modifie légèrement le script.
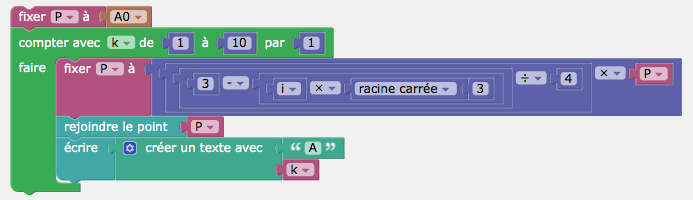
On peut vérifier que \(A3\) est sur la droite (Oy).
L'égalité \(\dfrac{z_{k+1} - z_{k}}{z_{k+1}} = - \dfrac{1}{\sqrt{3}}\text{i}\) montre que la ligne brisée est une sorte d'escargot de Pythagore avec\(A_kA_{k+1} = \dfrac{1}{\sqrt{3}} \text{O}A_{k+1}\).
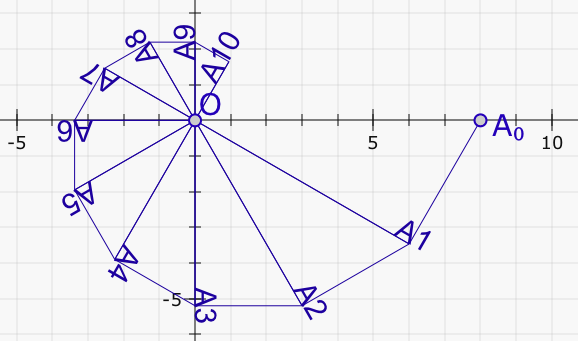
Pour obtenir cete figure, on a ajouté deux lignes dans le script tortue du point \(A_0\).
Enfin, on peut calculer et afficher la longueur de la ligne brisée.
On crée une expression L, et on ajuste le script tortue du point A.
On obtient cette figure dynamique.
